Developing a placental epigenetic risk score for maternal BMI
By Meredith Palmore, epigenetic risk score adapted from Ellen Howerton
Background
Maternal body mass index (BMI) is a known risk factor of child health outcomes, such as childhood obesity, preterm birth, and infant mortality. Additionally, the theory of biological embedding highlights that early life conditions, such as those conferred by maternal BMI, may contribute to healthfulness of offspring later in life. Despite the correlational evidence behind the impacts of maternal BMI on child health outcomes, fewer studies have examined the biological pathways linking maternal education to child health outcomes. There is a clear need to examine how biological pathways related to maternal prepregnancy BMI may contribute to later child health.
A plausible biological mechanism is epigenetic alterations to the placenta. The placenta mediates the transfer of life-supporting nutrients and stress signals to the developing fetus. Changes to the placental epigenome in the form of DNA methylation impact gene regulation and could serve as a biological mechanism for adverse infant health outcomes related to exposures during pregnancy. Both candidate gene studies and epigenome wide association studies (EWAS) have revealed relationships between maternal pre-pregnancy BMI and DNA methylation changes in the newborn epigenome. In this analysis, I aim to summarize the impact of maternal BMI on the fetal side of the placental epigenome in an epigenetic risk score. Capturing alterations to the infant epigenome during pregnancy in an epigenetic risk score will help to improve our understanding of the relationship between maternal BMI and adverse infant health outcomes. Understanding the biological risk of maternal BMI on infant health may influence the prioritization of public health initiatives and policies that target maternal health.
Description:
The primary goal of this analysis is to summarize the relationship between the infant epigenome and maternal BMI in a weighted epigenetic risk score. Predictors of epigenetic risk will be derived from summary statistics of a previous EWAS of pre-pregnancy BMI on placental DNA methylation. Epigenetic risk score performance will be validated in the RICHS cohort.
This function and following code show the DNA methylation scoring procedure for difference in M-value in placental tissue, comparing mothers with different BMI categories. The main scoring procedure is in the function, and then after all scoring is completed, the performance is evaluated and the results are plotted.
Some notes on the epigenetic risk score:
One of my colleagues, Ellen Howerton, kindly provided me with the function for the epigenetic risk score. I have modified it to work with categorical variables with multiple levels.
toppg_11 are the summary statistics derived from limma’s topTable() (rownames are CpG sites, column names are effect size of logFC, P.Value, etc.)
The M-value matrix, or the individual-level methylation data matrix, in this example is named M_regress
absmeans are the average of the absolute value of effect sizes.
Here, I have included one variable to score, BMI category, as well as scoring by p-value threshold, but it could be modified to be multiple variables and a CpG list to be more generalizable.
Wrangling the Data
Part 1. Load packages
library(tidyverse)
library(data.table)
library(reshape2)
library(here)
if (!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
#BiocManager::install("IlluminaHumanMethylation450kanno.ilmn12.hg19")
library(IlluminaHumanMethylation450kanno.ilmn12.hg19)
library(methyland) #A package for imputation that I made myself! It requires the Annotation file loaded above.
library(fmsb)
library(pROC)
library(readxl)
Part 2. Load in my M-value matrix and summary statistics
A couple of notes about the methylation data:
Here is a link to the study from which I derived summary statistics: https://pubmed.ncbi.nlm.nih.gov/32071425/
Here is a link to the study where I derived my GEO dataset: http://dx.doi.org/10.1080/15592294.2016.1195534
The summary statistics were derived from linear models adjusted for surrogate variables as proxy for placenta cellular heterogeneity, SNP-based ancestry principal components, methylation principal components, maternal age, race and ethnicity, offspring sex,and sequencing batches.
Both the summary statistics and methylation data are measured from placental tissue on the 450K methylation array.
Now I will load in the summary data for our risk score algorithm. There are multiple files for the summary statistics because they were converted from a pdf file.
#My top_11 frame (it's not a limma object, it's loaded in as a .csv)
setwd("C:/Users/softb/OneDrive - Johns Hopkins/Thesis/Data/Summ_stats_BMI/")
temp = list.files(pattern="*.csv")
myfiles = lapply(temp, read.csv)
for(i in 1:length(myfiles)){colnames(myfiles[[i]]) <- c("CpGs", "chrom", "logFC", "p-value", "direction")}
top_11 <- myfiles %>% bind_rows()
head(top_11)
CpGs chrom logFC p-value direction
1 cg10143030 chr2 0.004584571 0.2115875 Hypermethylat
2 cg07848601 chr5 0.009093954 0.2151436 Hypermethylat
3 cg26466094 chr1 -0.007766493 0.2162056 Hypomethylat
4 cg16724319 chr2 -0.050483370 0.2181015 Hypomethylat
5 cg22197787 chr1 -0.003223481 0.2339715 Hypomethylat
6 cg13266327 chr2 0.004322822 0.2374356 Hypermethylattop_11 <- as_tibble(top_11)
# Any missing data?
pMiss <- function(x){sum(is.na(x))/length(x)*100}
apply(top_11,2,pMiss)
CpGs chrom logFC p-value direction
0.00000000 0.00000000 0.05307856 0.00000000 0.00000000 # One logFC value missing, so I will remove it.
top_11 <- top_11[-c(which(is.na(top_11$logFC))),]
# Make all of the columns numeric:
colnames(top_11)
[1] "CpGs" "chrom" "logFC" "p-value" "direction"top_11$logFC <- as.numeric(top_11$logFC)
top_11$`p-value` <- as.numeric(top_11$`p-value`)
Now, I will load in the methylation data. We expect to see a data-frame with 237 subjects (columns) and a bit fewer than 450K rows of data corresponding to the CpG probes.
## My M-matrix:
setwd("C:/Users/softb/OneDrive - Johns Hopkins/Thesis/Data")
load("Mval_Matrix.rda")
dim(M_regress)
[1] 336484 237Part 3. Subset matrix to probes that transfer from the EPIC to 450K array
The methylation matrix from GEO is already cleaned. However, during the cleaning process, the authors filtered out many probes, inclusing ones with little variability in methylation. I need some of the probes that they filtered out.
There are two possible ways that I will deal with the probes that do not transfer: Either…
drop them from the analysis
find the nearest probes that we have measured and retain those for the score
I will try option 2. I wrote a function that will find the nearest probe for which we have methylation data measured, and return a list of those probes.
I developed an imputation function that finds the nearest probe on the array that is also in our dataset.
# # Option 2: Substitute missing with an imputation function I developed
missing_fromMatrix <- top_11[which(!top_11$CpGs %in% rownames(M_regress)), 1]
missing_fromMatrix <- deframe(missing_fromMatrix)
closest_probe <- findSub(missing_fromMatrix, M_regress, annotation= "Illumina450k")
closest_probe[,1] %in% rownames(M_regress)
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[14] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[27] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[40] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[53] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[66] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[79] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[92] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[105] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE # All TRUE! :)
# The first column are the probes that were substituted, the second is the nearest probe that my imputation function found. The third column is the distance between the two probes in base-pairs.
head(closest_probe)
Nearest_Probe Distance
cg13266327 "cg03997139" "9"
cg03393966 "cg10740054" "11"
cg15119377 "cg03518058" "82"
cg20227592 "cg13902024" "25384"
cg10442251 "cg23010629" "22"
cg07708472 "cg19807612" "50" # Subset M-matrix to these probes (all 50)
index_scoreprobes <- which(rownames(M_regress) %in% top_11$CpGs)
index_imputedprobes <- which(rownames(M_regress) %in% closest_probe[,1])
index_allprobes <- c(index_scoreprobes, index_imputedprobes)
M_regress <- M_regress[index_allprobes,]
#rename the substituted probes in the toptable
closest_probe <- tibble::rownames_to_column(as.data.frame(closest_probe), "CpGs")
top_11 <- left_join(top_11, closest_probe, by="CpGs")
top_11 <- top_11 %>% mutate(CpGs = ifelse(is.na(Nearest_Probe), CpGs, Nearest_Probe))
top_11 %>% select(CpGs, Nearest_Probe)
# A tibble: 1,883 x 2
CpGs Nearest_Probe
<chr> <chr>
1 cg10143030 <NA>
2 cg07848601 <NA>
3 cg26466094 <NA>
4 cg16724319 <NA>
5 cg22197787 <NA>
6 cg03997139 cg03997139
7 cg10740054 cg10740054
8 cg20594982 <NA>
9 cg05638699 <NA>
10 cg16274199 <NA>
# ... with 1,873 more rows[1] FALSE top_11<- top_11 %>% filter(duplicated(CpGs) == FALSE)
#Will keep the true (non-imputed) CpG because it has a stronger association and is located closer to the top of the list
Now that we have imputed the missing probes with nearby ones and updated them in the methylation matrix and in the top_11 object (summary statistics object), we can proceed with our computation of the score.
For the score, we must find the average absolute value of the logFC, or the log-fold change in methylation for each unit increase in BMI, and save it for later:
top_11$logFC <- as.numeric(top_11$logFC)
absmean_pg_11 <- mean(abs(top_11$logFC))
absmean_pg_11
[1] 0.005470551Part 4. Select individuals with phenotype information
The sample annotation file contains all the phenotypic data of the subjects in the RICHS cohort. We would expect that the rows in the phenotypic dataset correspond perfectly to the columns in the methylation dataset. Here, I will only retain the sample IDs and the outcome of interest, BMI.
Then, I calculate BMI categories because I need to be able to specify a reference group that I will compare mean methylation levels to, namely individuals with “normal” BMIs.
# Load in phenotype information
load("C:/Users/softb/OneDrive - Johns Hopkins/Thesis/Data/Subset_Annotation.rda")
pd <- subset_anno %>%
mutate("SampleID" = geo_accession, .before = geo_accession) %>%
select(SampleID, bmi)
#We expect to have 237 rows of data, corresponding with the 237 columns in the
head(pd)
SampleID bmi
GSM1947017 GSM1947017 39.91943
GSM1947018 GSM1947018 44.05074
GSM1947019 GSM1947019 19.60968
GSM1947020 GSM1947020 28.56811
GSM1947021 GSM1947021 21.31254
GSM1947023 GSM1947023 39.16633dim(pd)
[1] 237 2# Is there any missing data?
apply(pd,2,pMiss) # No.
SampleID bmi
0 0 # Divide BMI into categories.
pd$bmi <- as.numeric(pd$bmi)
pd = dplyr::mutate(pd, bmicat = cut(bmi, breaks = c(0,18.5, 25, 30,100), labels = 1:4, ordered = TRUE))
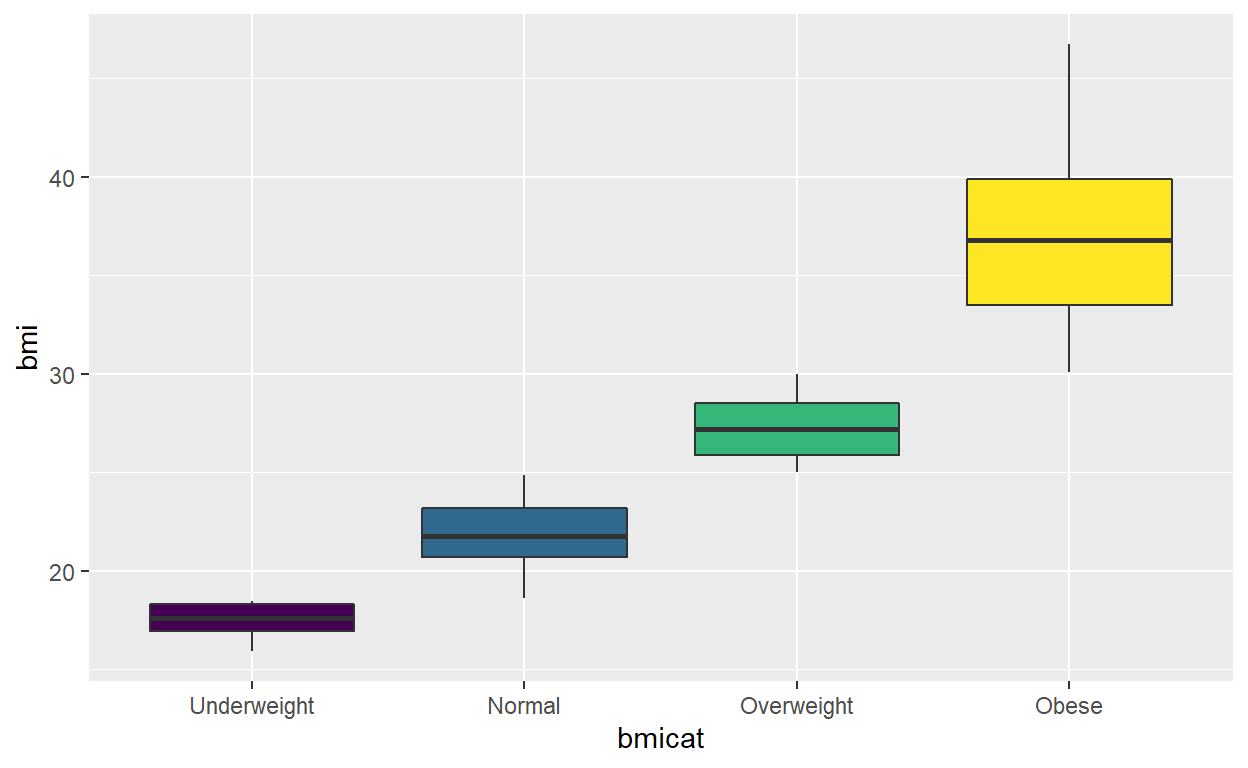
ggplot(pd, aes(bmicat, bmi, fill = bmicat)) +
geom_boxplot() +
scale_x_discrete(labels=c("1" = "Underweight", "2" = "Normal",
"3" = "Overweight", "4" = "Obese"))+
theme(legend.position= "none")
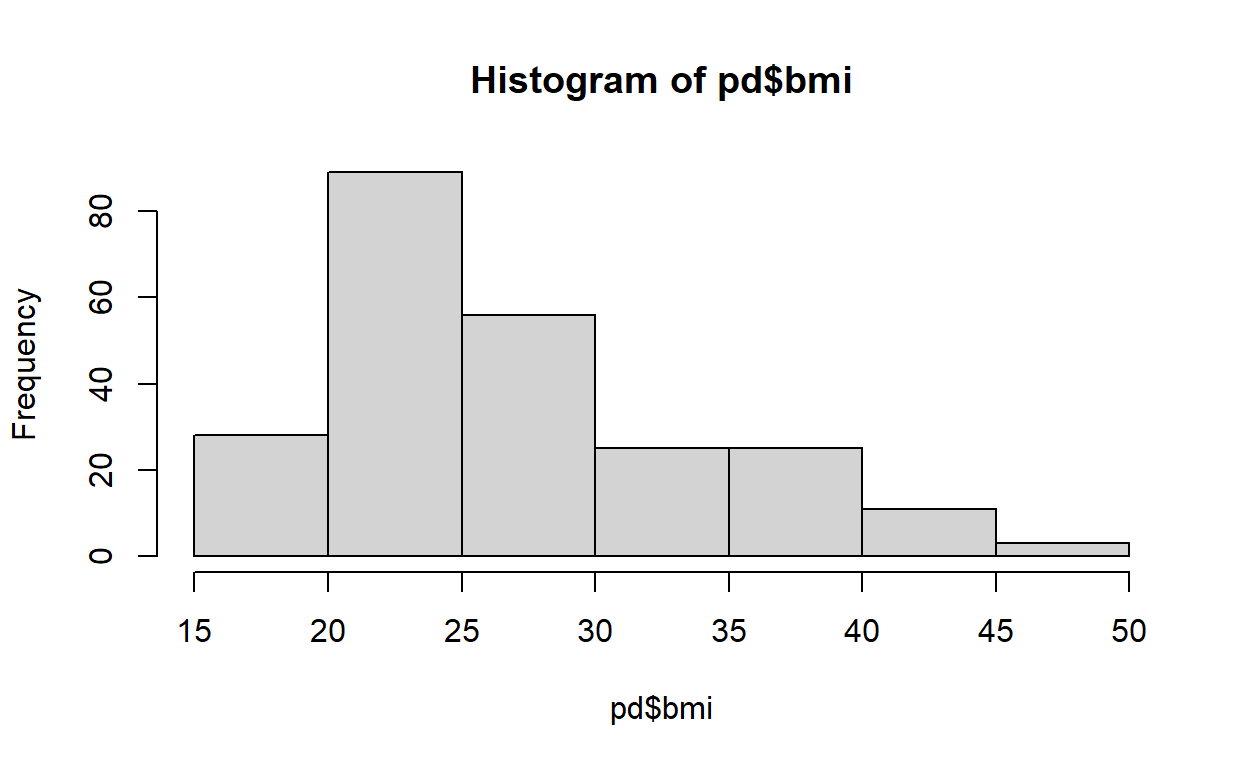
hist(pd$bmi) #Very right skewed
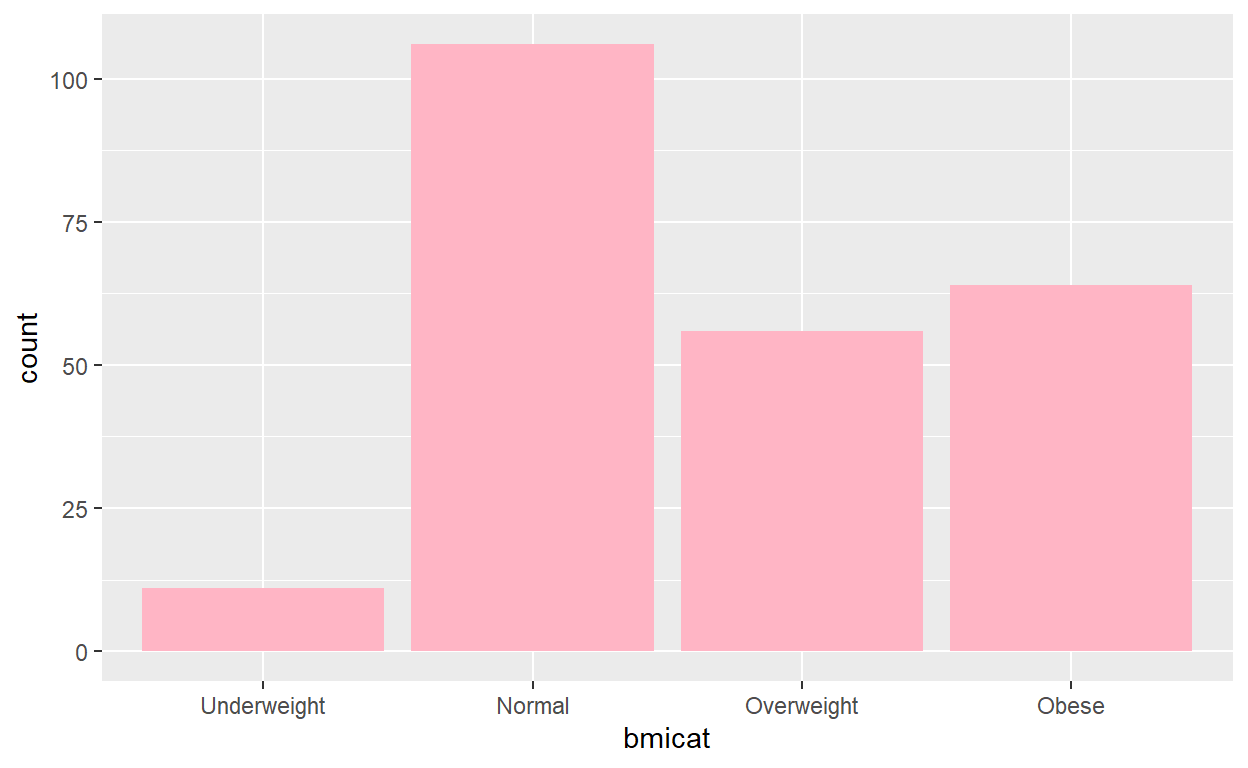
ggplot(pd, aes(bmicat)) +
geom_histogram(stat="count", fill = "pink1") +
scale_x_discrete(labels=c("1" = "Underweight", "2" = "Normal",
"3" = "Overweight", "4" = "Obese"))
class(pd$bmicat)
[1] "ordered" "factor" #Make sure there are 237 subjects in the sample annotation and the methylation data files.
dim(M_regress)
[1] 1869 237dim(pd)
[1] 237 3Run the epigenetic risk score function
Since the outcome is not binary, the baseline we are standardizing our methylation levels to are individuals with ‘normal’ BMI. So when comparing methylation to the the median value of the “unexposed”, the unexposed is individuals with normal BMI.
score_ts_byM_p <- function(variable, pthresh) {
top_11 <- top_11[top_11$`p-value` <= pthresh,]
top_11 <- mutate(top_11, CpG_site = CpGs)
top_11 <- top_11 %>%
as_tibble() %>%
dplyr::mutate(CpG_site = as.factor(CpG_site))
if(nrow(top_11) == 0) {
print(paste0("There are no CpGs that reached significance for p <= ", pthresh, ". Stopping function."))
stop()
}
print(paste0("Here are the CpG sites that have a p-value <= ", pthresh, ":"))
print(top_11)
fwrite(top_11, file.path("projects_files", paste0("cpg_list_in_score_", pthresh, "_", variable, ".csv")))
# prep count name
count_name <- paste0("count_", pthresh)
top_count_t_11 <- top_11 %>%
as_tibble() %>%
dplyr::mutate(CpG_site = as.factor(CpG_site)) %>%
dplyr::summarise(!!count_name := n(), total_CpGs = nrow(top_11))
print(top_count_t_11)
fwrite(top_count_t_11,file.path("projects_files",paste0("cpg_count_in_score_", pthresh, "_", variable, ".csv")))
# Note: Had to remove the directory specified because I don't have it.
# subset M-value matrix
t_cpg_site_names <- top_11 %>%
dplyr::select(CpG_site) %>%
dplyr::mutate(CpG_site = as.character(CpG_site)) %>%
deframe()
M_11 <- M_regress[t_cpg_site_names,] %>%
t() %>%
as.data.frame()
print("The dimensions of the M-value object, subsetted by CpG sites of interest:")
#print(head(M_11))
#print(tail(M_11))
print(dim(M_11))
# bind phenotype information
M_inf_11 <- cbind(M_11, pd[ ,c("SampleID","bmicat")])
print("The dimensions of the M-value object, with bmi information:")
#print(head(M_inf_11))
#print(tail(M_inf_11))
print(dim(M_inf_11))
M_inf_11 <- M_inf_11 %>%
dplyr::as_tibble()
#print("dimensions of the tibble:")
#print(dim(M_inf_11))
# reshape data to long
M_inf_melt_11 <- M_inf_11 %>%
#dplyr::as_tibble() %>%
melt(id.vars = c("SampleID","bmicat")) %>%
#dplyr::as_tibble() %>%
dplyr::rename(CpG_site = variable) %>%
dplyr::rename(M_value = value)
top_11$CpG_site <- as.character(top_11$CpG_site)
M_inf_melt_11$CpG_site <- as.character(M_inf_melt_11$CpG_site)
M_inf_melt_11 <- M_inf_melt_11 %>%
dplyr::left_join(top_11, by = "CpG_site")
print("The 'melted' M-value object, with bmi information:")
print(summary(M_inf_melt_11))
# empty median M value tibble
med_M <- tibble(CpG_site = factor(),
#timeframe = factor(),
med_M_unexp = numeric())
print("Check (empty) median M value tibble:")
print(med_M)
# for loop to add in median M value for the reference group (normal BMI = 2) for each CpG and time period
pd$bmicat <- as.numeric(pd$bmicat)
top_11$CpG_site <- as.factor(top_11$CpG_site)
for(i in seq_along(levels(top_11$CpG_site))) {
i_nm <- top_11$CpG_site[[i]]
row_M <- M_inf_melt_11 %>%
dplyr::mutate(CpG_site = as.factor(CpG_site)) %>%
dplyr::filter(CpG_site == i_nm & bmicat == 2) %>%
dplyr::summarize(CpG_site, med_M_unexp = median(M_value)) %>%
distinct()
med_M <- bind_rows(med_M, row_M)
}
print("Here is the median M-value of normal BMI (reference group) for all CpGs in the score:")
print(med_M)
# join the median unexposed to the melt score object
M_inf_melt_med <- dplyr::left_join(M_inf_melt_11, med_M, by = "CpG_site")
# print(M_inf_melt_med)
print("Check that median values joined correctly:")
print(summary(M_inf_melt_med))
# prep names for score columns
score_name <- paste0("score_", pthresh)
score_name <- gsub("e-", "E_", score_name)
# score!
M_inf_melt_score <- M_inf_melt_med %>%
dplyr::mutate(score_cpg = (logFC / absmean_pg_11) * (M_value - med_M_unexp)) %>%
dplyr::group_by(SampleID) %>%
dplyr::mutate(!!score_name := sum(score_cpg))
print(paste0("Scores are complete for the variable: ", variable, " and the p-value threshold of: ", pthresh))
# make more mergeable
M_inf_melt_score %>%
dplyr::select(SampleID, bmicat, !!score_name) %>%
distinct()
}
Results
Part 1. Make functions for results tables and graphs
Now that we have computed the scores, we can make functions for the results that include figures and regression results.
Functions make my code look nicer and more concise to have graphs summarizing the results from the risk score calculations.
gress_graph <- function(score){
indv_scores <- as.matrix(score[,3])
score$bmicat <- factor(score$bmicat, ordered = FALSE)
score$bmicat <- relevel(score$bmicat, ref = 2)
mod <- lm(indv_scores ~ bmicat, data = score)
mean_change <- coef(mod)
conf <- confint(mod)
print(mean_change)
print(conf)
print(summary(mod)$r.squared)
print(aic(mod))
ggplot(score, aes(x = bmicat, y = indv_scores)) +
geom_violin(fill = "pink1") +
geom_point(alpha=0.5) +
scale_x_discrete(labels=c("1" = "Underweight", "2" = "Normal",
"3" = "Overweight", "4" = "Obese"))
}
Part 2. Display the results
M_score_pg_1E_03 <- score_ts_byM_p("bmicat", 1*10^-3)
[1] "Here are the CpG sites that have a p-value <= 0.001:"
# A tibble: 2 x 8
CpGs chrom logFC `p-value` direction Nearest_Probe Distance
<chr> <chr> <dbl> <dbl> <chr> <chr> <chr>
1 cg13014558 chr11 -0.00603 0.000503 Hypometh~ <NA> <NA>
2 cg26947572 chr2 -0.0118 0.000723 Hypometh~ <NA> <NA>
# ... with 1 more variable: CpG_site <fct>
# A tibble: 1 x 2
count_0.001 total_CpGs
<int> <int>
1 2 2
[1] "The dimensions of the M-value object, subsetted by CpG sites of interest:"
[1] 237 2
[1] "The dimensions of the M-value object, with bmi information:"
[1] 237 4
[1] "The 'melted' M-value object, with bmi information:"
SampleID bmicat CpG_site M_value
Length:474 1: 22 Length:474 Min. :-6.02212
Class :character 2:212 Class :character 1st Qu.:-5.17617
Mode :character 3:112 Mode :character Median :-2.33216
4:128 Mean :-2.53902
3rd Qu.: 0.09552
Max. : 0.59106
CpGs chrom logFC
Length:474 Length:474 Min. :-0.011773
Class :character Class :character 1st Qu.:-0.011773
Mode :character Mode :character Median :-0.008900
Mean :-0.008900
3rd Qu.:-0.006027
Max. :-0.006027
p-value direction Nearest_Probe
Min. :0.0005027 Length:474 Length:474
1st Qu.:0.0005027 Class :character Class :character
Median :0.0006129 Mode :character Mode :character
Mean :0.0006129
3rd Qu.:0.0007231
Max. :0.0007231
Distance
Length:474
Class :character
Mode :character
[1] "Check (empty) median M value tibble:"
# A tibble: 0 x 2
# ... with 2 variables: CpG_site <fct>, med_M_unexp <dbl>
[1] "Here is the median M-value of normal BMI (reference group) for all CpGs in the score:"
# A tibble: 2 x 2
CpG_site med_M_unexp
<fct> <dbl>
1 cg13014558 0.0825
2 cg26947572 -5.20
[1] "Check that median values joined correctly:"
SampleID bmicat CpG_site M_value
Length:474 1: 22 Length:474 Min. :-6.02212
Class :character 2:212 Class :character 1st Qu.:-5.17617
Mode :character 3:112 Mode :character Median :-2.33216
4:128 Mean :-2.53902
3rd Qu.: 0.09552
Max. : 0.59106
CpGs chrom logFC
Length:474 Length:474 Min. :-0.011773
Class :character Class :character 1st Qu.:-0.011773
Mode :character Mode :character Median :-0.008900
Mean :-0.008900
3rd Qu.:-0.006027
Max. :-0.006027
p-value direction Nearest_Probe
Min. :0.0005027 Length:474 Length:474
1st Qu.:0.0005027 Class :character Class :character
Median :0.0006129 Mode :character Mode :character
Mean :0.0006129
3rd Qu.:0.0007231
Max. :0.0007231
Distance med_M_unexp
Length:474 Min. :-5.19757
Class :character 1st Qu.:-5.19757
Mode :character Median :-2.55752
Mean :-2.55752
3rd Qu.: 0.08254
Max. : 0.08254
[1] "Scores are complete for the variable: bmicat and the p-value threshold of: 0.001" gress_graph(M_score_pg_1E_03)
(Intercept) bmicat1 bmicat3 bmicat4
-0.02918356 0.08305977 -0.18809819 0.00519048
2.5 % 97.5 %
(Intercept) -0.1443039 0.085936813
bmicat1 -0.2923874 0.458506904
bmicat3 -0.3838995 0.007703169
bmicat4 -0.1824328 0.192813739
[1] 0.01970488
lik infl vari aic
-42.185102 3.433483 3.336728 91.237169 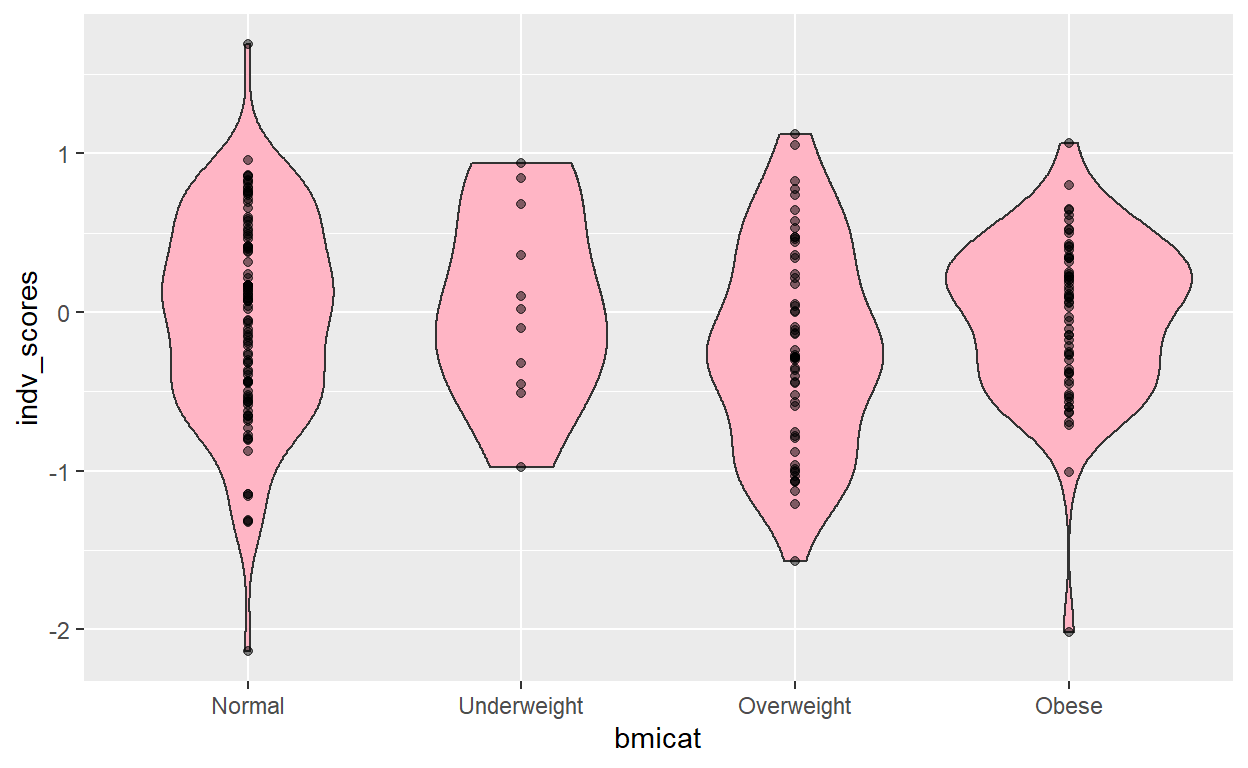
M_score_pg_1E_02 <- score_ts_byM_p("bmicat", 1*10^-2)
[1] "Here are the CpG sites that have a p-value <= 0.01:"
# A tibble: 53 x 8
CpGs chrom logFC `p-value` direction Nearest_Probe Distance
<chr> <chr> <dbl> <dbl> <chr> <chr> <chr>
1 cg13014~ chr11 -0.00603 0.000503 Hypomethy~ <NA> <NA>
2 cg26947~ chr2 -0.0118 0.000723 Hypomethy~ <NA> <NA>
3 cg05633~ chr2 0.0493 0.00108 Hypermeth~ <NA> <NA>
4 cg01054~ chr12 0.00608 0.00113 Hypermeth~ <NA> <NA>
5 cg12902~ chr1 -0.0327 0.00123 Hypomethy~ <NA> <NA>
6 cg11428~ chr22 0.0128 0.00157 Hypermeth~ <NA> <NA>
7 cg03719~ chr20 -0.0115 0.00160 Hypomethy~ <NA> <NA>
8 cg17492~ chr2 -0.0210 0.00167 Hypomethy~ <NA> <NA>
9 cg13782~ chr14 -0.0133 0.00170 Hypomethy~ <NA> <NA>
10 cg02759~ chr4 -0.0682 0.00172 Hypomethy~ <NA> <NA>
# ... with 43 more rows, and 1 more variable: CpG_site <fct>
# A tibble: 1 x 2
count_0.01 total_CpGs
<int> <int>
1 53 53
[1] "The dimensions of the M-value object, subsetted by CpG sites of interest:"
[1] 237 53
[1] "The dimensions of the M-value object, with bmi information:"
[1] 237 55
[1] "The 'melted' M-value object, with bmi information:"
SampleID bmicat CpG_site M_value
Length:12561 1: 583 Length:12561 Min. :-8.691
Class :character 2:5618 Class :character 1st Qu.:-5.480
Mode :character 3:2968 Mode :character Median :-4.998
4:3392 Mean :-3.688
3rd Qu.:-2.463
Max. : 5.809
CpGs chrom logFC
Length:12561 Length:12561 Min. :-0.068234
Class :character Class :character 1st Qu.:-0.014400
Mode :character Mode :character Median :-0.011544
Mean :-0.004837
3rd Qu.: 0.008676
Max. : 0.050861
p-value direction Nearest_Probe
Min. :0.0005027 Length:12561 Length:12561
1st Qu.:0.0021486 Class :character Class :character
Median :0.0037328 Mode :character Mode :character
Mean :0.0044511
3rd Qu.:0.0066821
Max. :0.0095655
Distance
Length:12561
Class :character
Mode :character
[1] "Check (empty) median M value tibble:"
# A tibble: 0 x 2
# ... with 2 variables: CpG_site <fct>, med_M_unexp <dbl>
[1] "Here is the median M-value of normal BMI (reference group) for all CpGs in the score:"
# A tibble: 53 x 2
CpG_site med_M_unexp
<fct> <dbl>
1 cg13014558 0.0825
2 cg26947572 -5.20
3 cg05633391 -5.41
4 cg01054110 1.95
5 cg12902497 -5.66
6 cg11428482 -5.59
7 cg03719642 2.19
8 cg17492041 -5.40
9 cg13782781 -5.06
10 cg02759110 -4.22
# ... with 43 more rows
[1] "Check that median values joined correctly:"
SampleID bmicat CpG_site M_value
Length:12561 1: 583 Length:12561 Min. :-8.691
Class :character 2:5618 Class :character 1st Qu.:-5.480
Mode :character 3:2968 Mode :character Median :-4.998
4:3392 Mean :-3.688
3rd Qu.:-2.463
Max. : 5.809
CpGs chrom logFC
Length:12561 Length:12561 Min. :-0.068234
Class :character Class :character 1st Qu.:-0.014400
Mode :character Mode :character Median :-0.011544
Mean :-0.004837
3rd Qu.: 0.008676
Max. : 0.050861
p-value direction Nearest_Probe
Min. :0.0005027 Length:12561 Length:12561
1st Qu.:0.0021486 Class :character Class :character
Median :0.0037328 Mode :character Mode :character
Mean :0.0044511
3rd Qu.:0.0066821
Max. :0.0095655
Distance med_M_unexp
Length:12561 Min. :-6.278
Class :character 1st Qu.:-5.427
Mode :character Median :-5.071
Mean :-3.704
3rd Qu.:-2.424
Max. : 5.042
[1] "Scores are complete for the variable: bmicat and the p-value threshold of: 0.01" gress_graph(M_score_pg_1E_02)
(Intercept) bmicat1 bmicat3 bmicat4
-5.477925 2.052503 2.507837 3.408030
2.5 % 97.5 %
(Intercept) -9.974812 -0.9810378
bmicat1 -12.613392 16.7183980
bmicat3 -5.140650 10.1563227
bmicat4 -3.920999 10.7370597
[1] 0.004094288
lik infl vari aic
-64335.112821 3.433483 3.336728 128677.092608 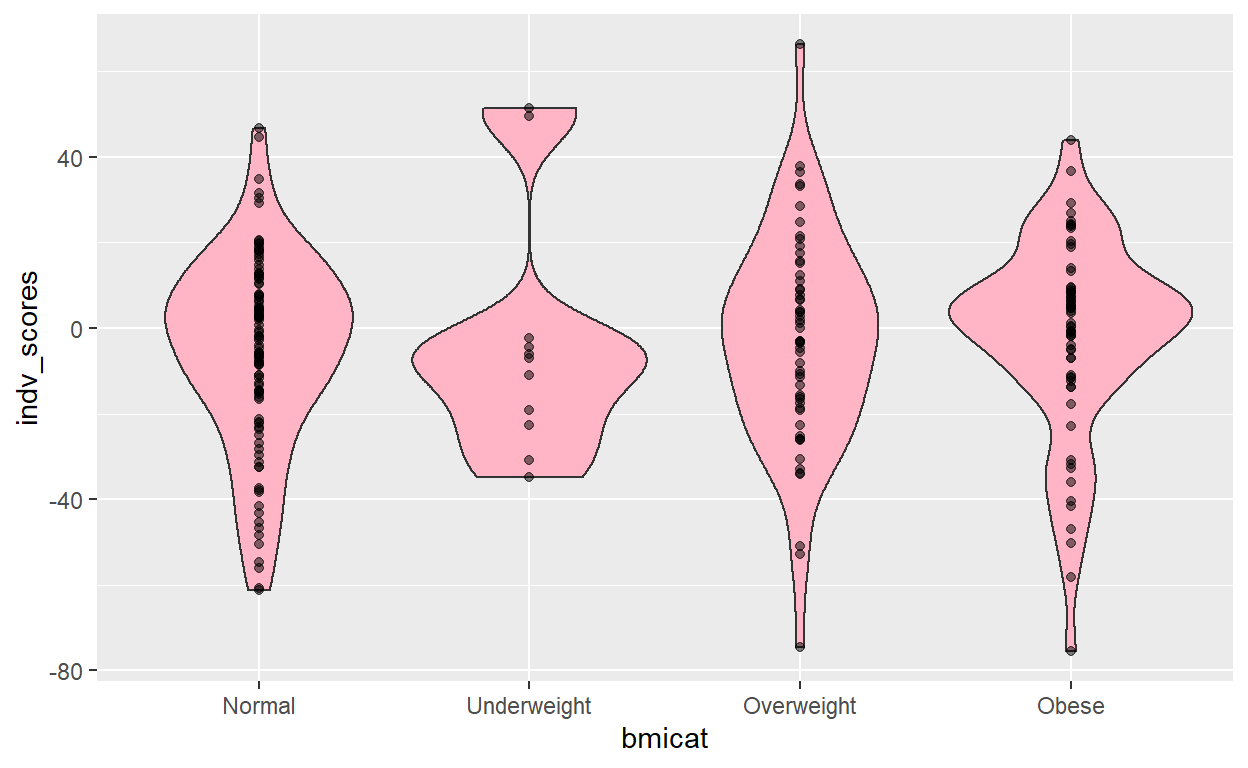
M_score_pg_1E_01 <- score_ts_byM_p("bmicat", 1*10^-1)
[1] "Here are the CpG sites that have a p-value <= 0.1:"
# A tibble: 312 x 8
CpGs chrom logFC `p-value` direction Nearest_Probe Distance
<chr> <chr> <dbl> <dbl> <chr> <chr> <chr>
1 cg13014~ chr11 -0.00603 0.000503 Hypomethy~ <NA> <NA>
2 cg26947~ chr2 -0.0118 0.000723 Hypomethy~ <NA> <NA>
3 cg05633~ chr2 0.0493 0.00108 Hypermeth~ <NA> <NA>
4 cg01054~ chr12 0.00608 0.00113 Hypermeth~ <NA> <NA>
5 cg12902~ chr1 -0.0327 0.00123 Hypomethy~ <NA> <NA>
6 cg11428~ chr22 0.0128 0.00157 Hypermeth~ <NA> <NA>
7 cg03719~ chr20 -0.0115 0.00160 Hypomethy~ <NA> <NA>
8 cg17492~ chr2 -0.0210 0.00167 Hypomethy~ <NA> <NA>
9 cg13782~ chr14 -0.0133 0.00170 Hypomethy~ <NA> <NA>
10 cg02759~ chr4 -0.0682 0.00172 Hypomethy~ <NA> <NA>
# ... with 302 more rows, and 1 more variable: CpG_site <fct>
# A tibble: 1 x 2
count_0.1 total_CpGs
<int> <int>
1 312 312
[1] "The dimensions of the M-value object, subsetted by CpG sites of interest:"
[1] 237 312
[1] "The dimensions of the M-value object, with bmi information:"
[1] 237 314
[1] "The 'melted' M-value object, with bmi information:"
SampleID bmicat CpG_site M_value
Length:73944 1: 3432 Length:73944 Min. :-9.173
Class :character 2:33072 Class :character 1st Qu.:-5.479
Mode :character 3:17472 Mode :character Median :-5.011
4:19968 Mean :-3.316
3rd Qu.:-1.815
Max. : 6.834
CpGs chrom logFC
Length:73944 Length:73944 Min. :-0.068234
Class :character Class :character 1st Qu.:-0.011853
Mode :character Mode :character Median :-0.007394
Mean :-0.003419
3rd Qu.: 0.007900
Max. : 0.050861
p-value direction Nearest_Probe
Min. :0.0005027 Length:73944 Length:73944
1st Qu.:0.0168901 Class :character Class :character
Median :0.0394770 Mode :character Mode :character
Mean :0.0439951
3rd Qu.:0.0709698
Max. :0.0995257
Distance
Length:73944
Class :character
Mode :character
[1] "Check (empty) median M value tibble:"
# A tibble: 0 x 2
# ... with 2 variables: CpG_site <fct>, med_M_unexp <dbl>
[1] "Here is the median M-value of normal BMI (reference group) for all CpGs in the score:"
# A tibble: 312 x 2
CpG_site med_M_unexp
<fct> <dbl>
1 cg13014558 0.0825
2 cg26947572 -5.20
3 cg05633391 -5.41
4 cg01054110 1.95
5 cg12902497 -5.66
6 cg11428482 -5.59
7 cg03719642 2.19
8 cg17492041 -5.40
9 cg13782781 -5.06
10 cg02759110 -4.22
# ... with 302 more rows
[1] "Check that median values joined correctly:"
SampleID bmicat CpG_site M_value
Length:73944 1: 3432 Length:73944 Min. :-9.173
Class :character 2:33072 Class :character 1st Qu.:-5.479
Mode :character 3:17472 Mode :character Median :-5.011
4:19968 Mean :-3.316
3rd Qu.:-1.815
Max. : 6.834
CpGs chrom logFC
Length:73944 Length:73944 Min. :-0.068234
Class :character Class :character 1st Qu.:-0.011853
Mode :character Mode :character Median :-0.007394
Mean :-0.003419
3rd Qu.: 0.007900
Max. : 0.050861
p-value direction Nearest_Probe
Min. :0.0005027 Length:73944 Length:73944
1st Qu.:0.0168901 Class :character Class :character
Median :0.0394770 Mode :character Mode :character
Mean :0.0439951
3rd Qu.:0.0709698
Max. :0.0995257
Distance med_M_unexp
Length:73944 Min. :-6.368
Class :character 1st Qu.:-5.468
Mode :character Median :-5.087
Mean :-3.312
3rd Qu.:-1.914
Max. : 5.611
[1] "Scores are complete for the variable: bmicat and the p-value threshold of: 0.1" gress_graph(M_score_pg_1E_01)
(Intercept) bmicat1 bmicat3 bmicat4
-8.293362 6.441864 2.134842 2.712726
2.5 % 97.5 %
(Intercept) -17.08768 0.500951
bmicat1 -22.23942 35.123144
bmicat3 -12.82288 17.092563
bmicat4 -11.62025 17.045704
[1] 0.001265498
lik infl vari aic
-2.460468e+05 3.433483e+00 3.336728e+00 4.921005e+05 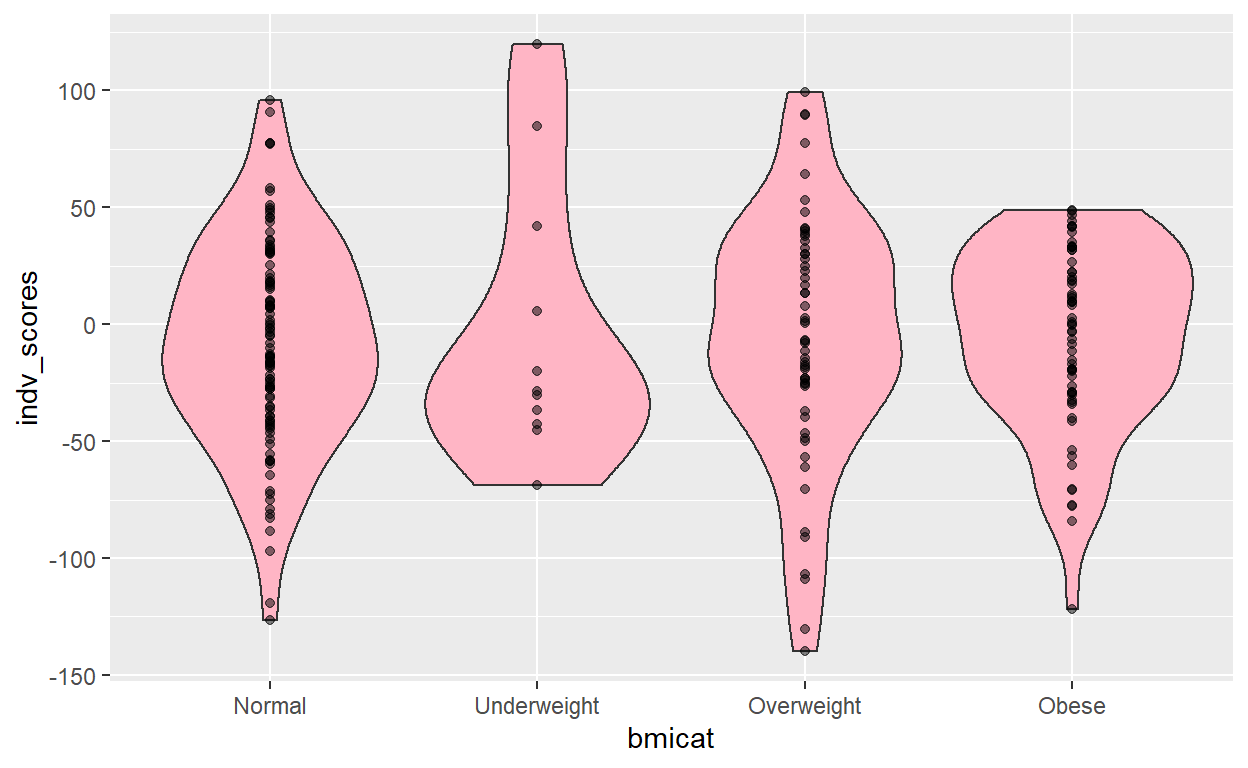
Discussion of the results
The model with the most stringent pruning threshold has the best discrimination, with an \(R^{2}\) of 2.0%. Additionally, since only 2 methylation loci were included, it was the most parsimonious model as well, with an AIC of just 91.24.
Additionally, the effect estimates are credible. Children with mothers with “normal” and “overweight” BMIs have comparable slight decrease in epigenetic risk scores, whereas those who were underweight had highest risk and those who were obese had the second highest epigenetic risk scores. Perhaps there are common epigenome-wide changes in individuals in the upper and lower extremes of BMI. This might extend to help explain observations of greater risks to conception-related outcomes in women who are on the extremes: e.g. in underweight, such as low birth-weight and preterm birth, as well as the risks for obese women such as infant mortality and preterm birth (Cnattingius et al., 1998).
However, I will caution that these results are not to be taken as truth. The effect sizes are quite small and not significant, and this is not a rigorous study, just a project. Additionally, risk scores are not to be taken for causal inference and every individual is different. Individual level outcomes may not always reflect what you would predict based on population level data.
Limitations:
This was an exploratory analysis for a self-directed project. If I were doing a real study, I might consider addressing the following:
I did not adjust for confounding factors in the validation set, but the effect estimates included in the risk score itself should be un-confounded, assuming the study where the summary statistics came from properly accounted for confounding. I think this is a fair assumption. Their quality control procedures were quite comprehensive!
I did not account for global differences in methylation, only single site changes. The normalization steps in the publicly available studies may have diluted global changes. Additionally, if there were differences in global methylation levels that are related to differences in characteristics of the 2 populations, then I may have obtained biased results.
Since I used publicly available data, I am a bit unclear about the specifics of the measurement of BMI in these cohorts. Additionally, I cannot look at other relevant exposures such as weight gain during pregnancy, so I may be missing some important information.
Future perspectives:
Here are some guiding questions for projects that would help contextualize and improve my analysis:
How much does the epigenetic risk score explain independently when included in a model with other covariates?
How is the risk score associated with child health outcomes?
Behavioral Risk Factors of Excessive Daytime Sleepiness in NHANES 2017-18
Background
Insufficient sleep duration and quality is associated with both morbidity and mortality from cardiometabolic disorders and affects neurobehavioral functioning (Gangwesh at al., 2006; Hall et al., 2008).
The 20th century has seen a downward trend in sleep duration and quality (Bixler, 2009).
Studies have identified health behaviors and personal characteristics that contribute to shortened sleep duration, such as age, race, obesity, low physical activity, heavy alcohol use, high caffeine consumption, smoking (Bixler, 2009; Phillips, 1995; Temple et al., 2017; Schoenborn & Adams, 2019; Stein & Friedmann, 2005; Kredlow, 2015).
Few research studies have sought to identify whether these relationships hold when the outcome is sleep quality rather than duration.
Sleep quality may be different from sleep duration. The sleep cycle is complex and sleep duration is not always indicative of high-quality sleep. In addition, sufficient sleep duration may also vary depending on the individual (Bin, 2016).
Understanding factors associated with poor sleep quality could provide insight to actionable avenues for intervention and ultimately impact quality of life, and even morbidity and mortality.
Study Design
Data were obtained from National Health and Nutritional Examination Survey (NHANES) 2017-2018, a cross-sectional complex survey. Home interviews and exams were conducted on a nationally representative sample of adults and children in the United States. A population-based sample was derived from a complex multistage, probability sampling design. 9,254 participants were interviewed, and 8,704 were examined. Only participants aged 18 and older were included in the analysis, resulting in a study sample size of 5,856.
Data
Since this is a risk factor study, all exposures were considered equally with no primary exposure of interest. Potential risk factors were derived from evidence in the literature. BMI and caffeine intake were measured in the examination stage. Alcohol use, excessive daytime sleepiness, current smoking, depression score, race and ethnicity, age, and participation in moderate to vigorous exercise were all collected at the interview stage. All risk factors except for income-to-poverty ratio, were transformed into categorical variables based on literature-informed criteria and conventions.
Excessive daytime sleepiness was chosen as the outcome of interest. This outcome was selected over self-reported hours of sleep because it is an indicator of sleep quality, rather than sleep duration. The question asked to participants was “In the past month, how often did {you/survey participant} feel excessively or overly sleepy during the day?” Following the convention of Lal et al., participants responded as “Often” or “Almost always” were categorized as “Yes,” and other responses were categorized as “No. This study was exploratory in nature and meant to be hypothesis-generating and replicate prior associations between behavioral risk factors and sleep quality.
Wrangling the data
First, I will load in the packages that I will use for my analysis.
Now, I will read in my datasets. I exported the data from the NHANES 2018 website and converted them to .csv files. I will load them all and combine them into a larger file. I will merge all of the component files by the individuals’ identifying number (SEQN). I decide to left join with demography file as the leftmost column, because I want to retain the denominator of individuals even if some the predictor and outcome variables are missing.
temp = list.files(".","*.csv")
myfiles = lapply(temp, read.csv)
one_tmp <- myfiles[[5]] #This is the demographic dataset
for(i in c(1:4,6:8)){
one_tmp <- left_join(one_tmp, myfiles[[i]], by = "SEQN")
}
# Fix the naming of some of these variables:
head(one_tmp)
X.x SEQN RIAGENDR RIDAGEYR RIDRETH3 WTINT2YR WTMEC2YR SDMVPSU
1 1 93703 2 2 6 9246.492 8539.731 2
2 2 93704 1 2 3 37338.768 42566.615 1
3 3 93705 2 66 4 8614.571 8338.420 2
4 4 93706 1 18 6 8548.633 8723.440 2
5 5 93707 1 13 7 6769.345 7064.610 1
6 6 93708 2 66 6 13329.451 14372.489 2
SDMVSTRA INDFMPIR X.y PAQ605 PAQ620 PAQ650 PAQ665 X.x.x ALQ111
1 145 5.00 NA NA NA NA NA NA NA
2 143 5.00 NA NA NA NA NA NA NA
3 145 0.82 1 2 2 2 1 1 1
4 134 NA 2 2 2 2 1 2 2
5 138 1.88 NA NA NA NA NA NA NA
6 138 1.63 3 2 2 2 1 3 2
ALQ121 ALQ130 X.y.y BMXBMI X.x.x.x DR1TCAFF DR2TCAFF
1 NA NA 1 17.5 1 NA NA
2 NA NA 2 15.7 2 8 6
3 7 1 3 31.7 3 361 146
4 NA NA 4 21.5 4 0 NA
5 NA NA 5 18.1 5 21 10
6 NA NA 6 23.7 6 33 0
avg_mg_caffeine X.y.y.y DPQ010 DPQ020 DPQ030 DPQ040 DPQ050 DPQ060
1 NA NA NA NA NA NA NA NA
2 7.0 NA NA NA NA NA NA NA
3 253.5 1 0 0 0 0 0 0
4 NA 2 0 0 0 0 0 0
5 15.5 NA NA NA NA NA NA NA
6 16.5 3 0 0 0 0 0 0
DPQ070 DPQ080 DPQ090 DPQ100 X.x.x.x.x SLD012 SLD013 SLQ120
1 NA NA NA NA NA NA NA NA
2 NA NA NA NA NA NA NA NA
3 0 0 0 NA 1 8.0 8.0 0
4 0 0 0 NA 2 10.5 11.5 1
5 NA NA NA NA NA NA NA NA
6 0 0 0 NA 3 8.0 8.0 2
day_sleep X.y.y.y.y SMQ681
1 NA NA NA
2 NA NA NA
3 0 1 2
4 0 2 2
5 NA 3 2
6 0 4 2# A tibble: 6 x 35
SEQN RIAGENDR RIDAGEYR RIDRETH3 WTINT2YR WTMEC2YR SDMVPSU SDMVSTRA
<dbl> <int> <int> <int> <dbl> <dbl> <int> <int>
1 93703 2 2 6 9246. 8540. 2 145
2 93704 1 2 3 37339. 42567. 1 143
3 93705 2 66 4 8615. 8338. 2 145
4 93706 1 18 6 8549. 8723. 2 134
5 93707 1 13 7 6769. 7065. 1 138
6 93708 2 66 6 13329. 14372. 2 138
# ... with 27 more variables: INDFMPIR <dbl>, PAQ605 <int>,
# PAQ620 <int>, PAQ650 <int>, PAQ665 <int>, ALQ111 <int>,
# ALQ121 <int>, ALQ130 <int>, BMXBMI <dbl>, DR1TCAFF <int>,
# DR2TCAFF <int>, avg_mg_caffeine <dbl>, DPQ010 <int>,
# DPQ020 <int>, DPQ030 <int>, DPQ040 <int>, DPQ050 <int>,
# DPQ060 <int>, DPQ070 <int>, DPQ080 <int>, DPQ090 <int>,
# DPQ100 <int>, SLD012 <dbl>, SLD013 <dbl>, SLQ120 <int>, ...# Worked beautifully!
Some of the data are labeled as numeric values if they were missing. Referring to NHANES documentation, you can see which numbers correspond to missing data, depending on the variable. It would be a good idea to convert them into simple NAs.
one_tmp <- one_tmp %>%
mutate(across(starts_with('ALQ'), ~ case_when(. == 77 ~ NA_integer_, . == 99 ~ NA_integer_, . == 777 ~ NA_integer_, . == 999 ~ NA_integer_, TRUE ~ as.integer(.))))
#For activity variables, change to missing if "Refused" or "Don't Know"
one_tmp <- one_tmp %>%
mutate(across(starts_with('PAQ'), ~ case_when(. == 9 ~ NA_integer_, TRUE ~ as.integer(.))))
#For depression variables, change to missing if "Refused" or "Don't Know"
one_tmp <- one_tmp %>%
mutate(across(starts_with('DPQ'), ~ case_when(. == 7 ~ NA_integer_, . == 9 ~ NA_integer_, TRUE ~ as.integer(.))))
summary(one_tmp) # Looking better.
SEQN RIAGENDR RIDAGEYR RIDRETH3
Min. : 93703 Min. :1.000 Min. : 0.00 Min. :1.000
1st Qu.: 96016 1st Qu.:1.000 1st Qu.:11.00 1st Qu.:3.000
Median : 98330 Median :2.000 Median :31.00 Median :3.000
Mean : 98330 Mean :1.508 Mean :34.33 Mean :3.497
3rd Qu.:100643 3rd Qu.:2.000 3rd Qu.:58.00 3rd Qu.:4.000
Max. :102956 Max. :2.000 Max. :80.00 Max. :7.000
WTINT2YR WTMEC2YR SDMVPSU SDMVSTRA
Min. : 2571 Min. : 0 Min. :1.000 Min. :134
1st Qu.: 13074 1st Qu.: 12347 1st Qu.:1.000 1st Qu.:137
Median : 21099 Median : 21060 Median :2.000 Median :141
Mean : 34671 Mean : 34671 Mean :1.518 Mean :141
3rd Qu.: 36923 3rd Qu.: 37562 3rd Qu.:2.000 3rd Qu.:145
Max. :433085 Max. :419763 Max. :2.000 Max. :148
INDFMPIR PAQ605 PAQ620 PAQ650
Min. :0.000 Min. :1.000 Min. :1.000 Min. :1.000
1st Qu.:1.040 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:2.000
Median :1.920 Median :2.000 Median :2.000 Median :2.000
Mean :2.376 Mean :1.763 Mean :1.583 Mean :1.755
3rd Qu.:3.690 3rd Qu.:2.000 3rd Qu.:2.000 3rd Qu.:2.000
Max. :5.000 Max. :2.000 Max. :2.000 Max. :2.000
NA's :1231 NA's :3404 NA's :3403 NA's :3398
PAQ665 ALQ111 ALQ121 ALQ130
Min. :1.000 Min. :1.000 Min. : 0.000 Min. : 1.000
1st Qu.:1.000 1st Qu.:1.000 1st Qu.: 1.000 1st Qu.: 1.000
Median :2.000 Median :1.000 Median : 5.000 Median : 2.000
Mean :1.606 Mean :1.114 Mean : 4.911 Mean : 2.517
3rd Qu.:2.000 3rd Qu.:1.000 3rd Qu.: 8.000 3rd Qu.: 3.000
Max. :2.000 Max. :2.000 Max. :10.000 Max. :15.000
NA's :3398 NA's :4124 NA's :4713 NA's :5765
BMXBMI DR1TCAFF DR2TCAFF avg_mg_caffeine
Min. :12.30 Min. : 0.0 Min. : 0.00 Min. : 0.00
1st Qu.:20.40 1st Qu.: 1.0 1st Qu.: 0.00 1st Qu.: 2.50
Median :25.80 Median : 35.0 Median : 26.00 Median : 40.00
Mean :26.58 Mean : 100.2 Mean : 88.68 Mean : 94.79
3rd Qu.:31.30 3rd Qu.: 143.0 3rd Qu.: 127.00 3rd Qu.: 135.50
Max. :86.20 Max. :4320.0 Max. :5040.00 Max. :4680.00
NA's :1249 NA's :1770 NA's :2752 NA's :2763
DPQ010 DPQ020 DPQ030 DPQ040
Min. :0.000 Min. :0.00 Min. :0.000 Min. :0.000
1st Qu.:0.000 1st Qu.:0.00 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 Median :0.00 Median :0.000 Median :0.000
Mean :0.387 Mean :0.35 Mean :0.636 Mean :0.752
3rd Qu.:1.000 3rd Qu.:0.00 3rd Qu.:1.000 3rd Qu.:1.000
Max. :3.000 Max. :3.00 Max. :3.000 Max. :3.000
NA's :4168 NA's :4167 NA's :4168 NA's :4169
DPQ050 DPQ060 DPQ070 DPQ080
Min. :0.000 Min. :0.000 Min. :0.000 Min. :0.000
1st Qu.:0.000 1st Qu.:0.000 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 Median :0.000 Median :0.000 Median :0.000
Mean :0.392 Mean :0.244 Mean :0.264 Mean :0.168
3rd Qu.:1.000 3rd Qu.:0.000 3rd Qu.:0.000 3rd Qu.:0.000
Max. :3.000 Max. :3.000 Max. :3.000 Max. :3.000
NA's :4167 NA's :4171 NA's :4168 NA's :4170
DPQ090 DPQ100 SLD012 SLD013
Min. :0.000 Min. :0.000 Min. : 2.000 Min. : 2.000
1st Qu.:0.000 1st Qu.:0.000 1st Qu.: 7.000 1st Qu.: 7.000
Median :0.000 Median :0.000 Median : 8.000 Median : 8.000
Mean :0.053 Mean :0.321 Mean : 7.659 Mean : 8.378
3rd Qu.:0.000 3rd Qu.:1.000 3rd Qu.: 8.500 3rd Qu.: 9.500
Max. :3.000 Max. :3.000 Max. :14.000 Max. :14.000
NA's :4169 NA's :5895 NA's :3141 NA's :3150
SLQ120 day_sleep SMQ681
Min. :0.000 Min. :0.0000 Min. :1.00
1st Qu.:1.000 1st Qu.:0.0000 1st Qu.:2.00
Median :2.000 Median :0.0000 Median :2.00
Mean :1.786 Mean :0.2587 Mean :1.81
3rd Qu.:3.000 3rd Qu.:1.0000 3rd Qu.:2.00
Max. :9.000 Max. :1.0000 Max. :2.00
NA's :3093 NA's :3093 NA's :3301 Categorize variables based on clinically meaningful guidelines
Now I create a summary depression score by summing all question responses except for DPQ100, which was more of a measure of life quality than magnitude of depression.
Now I turn depression into a categorical variable
Depression is categorized based on guidelines:
- No depression: no_dep = 1 if total score <5; 0 if total score >= 5.
- Mild depression: mild_dep = 1 if total score <10 and >4; 0 otherwise.
- Moderate depression: mod_dep = 1 if total score >9 and <15; 0 therwise
- Moderate to severe: mod_sev_dep = 1 if total score >14 and <20; 0 otherwise
- Severe: sev_dep = 1 if total score >19; 0 otherwise
Create race and Hispanic ethnicity categories. Combined Non-Hispanic white and Non-Hispanic other and multiple races, to approximate the sampling domains.
one_tmp = one_tmp %>% mutate(
race1 = factor(c(3, 3, 4, 1, NA, 2, 4)[RIDRETH3],
labels = c('NH Black','NH Asian', 'Hispanic', 'NH White and Other')),
# Create race and Hispanic ethnicity categories for hypertension analysis
raceEthCat= factor(c(4, 4, 1, 2, NA, 3, 5)[RIDRETH3],
labels = c('NH White', 'NH Black', 'NH Asian', 'Hispanic', 'NH Other/Multiple')),
# Create age categories for adults aged 18 and over: ages 18-39, 40-59, 60 and over
ageCat_18 = cut(RIDAGEYR, breaks = c(17, 39, 59, Inf),
labels = c('18-39','40-59','60+'))
)
Regular moderate or vigorous activity reported? 1 = yes; 0 = no
Recommended caffeine dose is 400 mg. Dichotomize to above and below that threshold:
There are standards for categorizing BMI. I will carry them out here:
Categorize alcohol use
Above 2 drinks a day for men or above 1 drink a day for women are considered in excess of “moderate drinking”. https://www.niaaa.nih.gov/alcohol-health/overview-alcohol-consumption/moderate-binge-drinking
Must account for those who responded that they were non-drinkers. Re-code alcohol consumption accounting for those who don’t drink to correct missingness
I will filter the population to ages 18 and above and save in a new dataset for analysis. I do this for 2 reasons. First, I would like the analytic population to be adults only. Second, the measurement of variables in NHANES is different in children.
unweighted_data <- filter(one_tmp, RIDAGEYR >=18)
Correcting for missingness
How many are missing a the conventional 10% cutoff?
missing <- colSums(is.na(unweighted_data))# Number of missing per variable
missing <- missing/(length(unweighted_data$SEQN))
missing
SEQN RIAGENDR RIDAGEYR RIDRETH3
0.0000000000 0.0000000000 0.0000000000 0.0000000000
WTINT2YR WTMEC2YR SDMVPSU SDMVSTRA
0.0000000000 0.0000000000 0.0000000000 0.0000000000
INDFMPIR PAQ605 PAQ620 PAQ650
0.1425887978 0.0010245902 0.0008538251 0.0000000000
PAQ665 ALQ111 ALQ121 ALQ130
0.0000000000 0.1239754098 0.2245560109 0.4042008197
BMXBMI DR1TCAFF DR2TCAFF avg_mg_caffeine
0.0720628415 0.1490778689 0.2590505464 0.2590505464
DPQ010 DPQ020 DPQ030 DPQ040
0.1314890710 0.1313183060 0.1314890710 0.1316598361
DPQ050 DPQ060 DPQ070 DPQ080
0.1313183060 0.1320013661 0.1314890710 0.1318306011
DPQ090 DPQ100 SLD012 SLD013
0.1316598361 0.4264002732 0.0080259563 0.0095628415
SLQ120 day_sleep SMQ681 depress_score
0.0000000000 0.0000000000 0.1236338798 0.1345628415
depress_cat race1 raceEthCat ageCat_18
0.1345628415 0.0000000000 0.0000000000 0.0000000000
activity hi_caffeine BMI_cat heavy_drink
0.0011953552 0.2590505464 0.0720628415 0.4042008197
heavy_drink2
0.1256830601 Missingness: No individuals were missing the outcome. Missingness was below 15% for all covariates except for high caffeine intake, which was missing at a rate of 26%.
Now that we have cleaned the NHANES data to our liking, it is time to conduct the analysis.
Let’s load the packages that we will need. Must load the tidyverse last because both the dplyr package from the tidyverse and the MASS package have a select() function and the one loaded last is the one that will be used.
if(!require(car)){ # for added variable plots, VIF
install.packages("car")
library(car)
}
if(!require(sandwich)){ # for robust linear regression
install.packages("sandwich")
library(sandwich)
}
if(!require(GGally)){ # for fancier scatterplot matrices
install.packages("GGally")
library(GGally)
}
if(!require(broom)){ # for tidy model output using tidy() function
install.packages("broom")
library(broom)
}
if(!require(lmtest)){ # coefficient test for robust variance
install.packages("lmtest")
library(lmtest)
}
if(!require(tidyverse)){ # general functions for working with data
install.packages("tidyverse")
library(tidyverse)
}
if(!require(survey)){ # general functions for working with data
install.packages("survey")
library(survey)
}
Subset the dataset to individuals 18 and older, because that is the population we would like to make inferences to.
SEQN RIAGENDR RIDAGEYR RIDRETH3
Min. : 93703 Min. :1.000 Min. : 0.00 Min. :1.000
1st Qu.: 96016 1st Qu.:1.000 1st Qu.:11.00 1st Qu.:3.000
Median : 98330 Median :2.000 Median :31.00 Median :3.000
Mean : 98330 Mean :1.508 Mean :34.33 Mean :3.497
3rd Qu.:100643 3rd Qu.:2.000 3rd Qu.:58.00 3rd Qu.:4.000
Max. :102956 Max. :2.000 Max. :80.00 Max. :7.000
WTINT2YR WTMEC2YR SDMVPSU SDMVSTRA
Min. : 2571 Min. : 0 Min. :1.000 Min. :134
1st Qu.: 13074 1st Qu.: 12347 1st Qu.:1.000 1st Qu.:137
Median : 21099 Median : 21060 Median :2.000 Median :141
Mean : 34671 Mean : 34671 Mean :1.518 Mean :141
3rd Qu.: 36923 3rd Qu.: 37562 3rd Qu.:2.000 3rd Qu.:145
Max. :433085 Max. :419763 Max. :2.000 Max. :148
INDFMPIR PAQ605 PAQ620 PAQ650
Min. :0.000 Min. :1.000 Min. :1.000 Min. :1.000
1st Qu.:1.040 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:2.000
Median :1.920 Median :2.000 Median :2.000 Median :2.000
Mean :2.376 Mean :1.763 Mean :1.583 Mean :1.755
3rd Qu.:3.690 3rd Qu.:2.000 3rd Qu.:2.000 3rd Qu.:2.000
Max. :5.000 Max. :2.000 Max. :2.000 Max. :2.000
NA's :1231 NA's :3404 NA's :3403 NA's :3398
PAQ665 ALQ111 ALQ121 ALQ130
Min. :1.000 Min. :1.000 Min. : 0.000 Min. : 1.000
1st Qu.:1.000 1st Qu.:1.000 1st Qu.: 1.000 1st Qu.: 1.000
Median :2.000 Median :1.000 Median : 5.000 Median : 2.000
Mean :1.606 Mean :1.114 Mean : 4.911 Mean : 2.517
3rd Qu.:2.000 3rd Qu.:1.000 3rd Qu.: 8.000 3rd Qu.: 3.000
Max. :2.000 Max. :2.000 Max. :10.000 Max. :15.000
NA's :3398 NA's :4124 NA's :4713 NA's :5765
BMXBMI DR1TCAFF DR2TCAFF avg_mg_caffeine
Min. :12.30 Min. : 0.0 Min. : 0.00 Min. : 0.00
1st Qu.:20.40 1st Qu.: 1.0 1st Qu.: 0.00 1st Qu.: 2.50
Median :25.80 Median : 35.0 Median : 26.00 Median : 40.00
Mean :26.58 Mean : 100.2 Mean : 88.68 Mean : 94.79
3rd Qu.:31.30 3rd Qu.: 143.0 3rd Qu.: 127.00 3rd Qu.: 135.50
Max. :86.20 Max. :4320.0 Max. :5040.00 Max. :4680.00
NA's :1249 NA's :1770 NA's :2752 NA's :2763
DPQ010 DPQ020 DPQ030 DPQ040
Min. :0.000 Min. :0.00 Min. :0.000 Min. :0.000
1st Qu.:0.000 1st Qu.:0.00 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 Median :0.00 Median :0.000 Median :0.000
Mean :0.387 Mean :0.35 Mean :0.636 Mean :0.752
3rd Qu.:1.000 3rd Qu.:0.00 3rd Qu.:1.000 3rd Qu.:1.000
Max. :3.000 Max. :3.00 Max. :3.000 Max. :3.000
NA's :4168 NA's :4167 NA's :4168 NA's :4169
DPQ050 DPQ060 DPQ070 DPQ080
Min. :0.000 Min. :0.000 Min. :0.000 Min. :0.000
1st Qu.:0.000 1st Qu.:0.000 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 Median :0.000 Median :0.000 Median :0.000
Mean :0.392 Mean :0.244 Mean :0.264 Mean :0.168
3rd Qu.:1.000 3rd Qu.:0.000 3rd Qu.:0.000 3rd Qu.:0.000
Max. :3.000 Max. :3.000 Max. :3.000 Max. :3.000
NA's :4167 NA's :4171 NA's :4168 NA's :4170
DPQ090 DPQ100 SLD012 SLD013
Min. :0.000 Min. :0.000 Min. : 2.000 Min. : 2.000
1st Qu.:0.000 1st Qu.:0.000 1st Qu.: 7.000 1st Qu.: 7.000
Median :0.000 Median :0.000 Median : 8.000 Median : 8.000
Mean :0.053 Mean :0.321 Mean : 7.659 Mean : 8.378
3rd Qu.:0.000 3rd Qu.:1.000 3rd Qu.: 8.500 3rd Qu.: 9.500
Max. :3.000 Max. :3.000 Max. :14.000 Max. :14.000
NA's :4169 NA's :5895 NA's :3141 NA's :3150
SLQ120 day_sleep SMQ681 depress_score
Min. :0.000 Min. :0.0000 Min. :1.00 Min. : 0.000
1st Qu.:1.000 1st Qu.:0.0000 1st Qu.:2.00 1st Qu.: 0.000
Median :2.000 Median :0.0000 Median :2.00 Median : 2.000
Mean :1.786 Mean :0.2587 Mean :1.81 Mean : 3.241
3rd Qu.:3.000 3rd Qu.:1.0000 3rd Qu.:2.00 3rd Qu.: 5.000
Max. :9.000 Max. :1.0000 Max. :2.00 Max. :25.000
NA's :3093 NA's :3093 NA's :3301 NA's :4186
depress_cat race1
nodep :3772 NH Black :2115
mild_dep : 837 NH Asian :1168
mod_dep : 292 Hispanic :2187
mod_sev_dep: 124 NH White and Other:3784
sev_dep : 43
NA's :4186
raceEthCat ageCat_18 activity
NH White :3150 18-39:1974 Min. :0.000
NH Black :2115 40-59:1732 1st Qu.:0.000
NH Asian :1168 60+ :2150 Median :1.000
Hispanic :2187 NA's :3398 Mean :0.675
NH Other/Multiple: 634 3rd Qu.:1.000
Max. :1.000
NA's :3405
hi_caffeine BMI_cat heavy_drink heavy_drink2
Min. :0.000 underweight:1449 Min. :0.000 Min. :0.000
1st Qu.:0.000 normal :2191 1st Qu.:0.000 1st Qu.:0.000
Median :0.000 overweight :1957 Median :0.000 Median :0.000
Mean :0.034 obese :2408 Mean :0.482 Mean :0.329
3rd Qu.:0.000 NA's :1249 3rd Qu.:1.000 3rd Qu.:1.000
Max. :1.000 Max. :1.000 Max. :1.000
NA's :2763 NA's :5765 NA's :4134
inAnalysis
Mode :logical
FALSE:3398
TRUE :5856
Now, we would like to specify the categorical data as either nominal or ordinal data for our models. BMI categories, race, and age groups should be considered separately as nominal categories. Depression questionnaire scores have a natural ordered relationship, so we will specify the depression variable as an ordinal variable.
We must also set a reference group for the generalized linear models to improve our interpretations.
#Nominal variables
data$BMI_cat <- factor(data$BMI_cat, ordered = FALSE )
data$raceEthCat <- factor(data$raceEthCat, ordered = FALSE )
data$ageCat_18 <- factor(data$ageCat_18, ordered = FALSE)
#Set reference groups for statistical models
data <- within(data, raceEthCat <- relevel(raceEthCat, ref = "NH White"))
data <- within(data, BMI_cat <- relevel(BMI_cat, ref = "normal"))
data <- within(data, ageCat_18 <- relevel(ageCat_18, ref = "18-39"))
# Ordinal variables
data$depress_cat <- ordered(data$depress_cat, levels = c("nodep","mild_dep","mod_dep","mod_sev_dep","sev_dep"))
Table 1
I will make a table of descriptive statistics, stratified by the outcome, daytime sleepiness.
library(tableone)
listVars <- c("RIAGENDR", "ageCat_18", "INDFMPIR", "SMQ681", "raceEthCat", "activity", "hi_caffeine", "BMI_cat", "heavy_drink2", "depress_cat")
catVars <- c("RIAGENDR", "ageCat_18", "SMQ681", "raceEthCat", "activity", "hi_caffeine", "BMI_cat", "heavy_drink2", "depress_cat")
table1 <- CreateTableOne(vars = listVars, data = unweighted_data, factorVars = catVars, strata=c("day_sleep"))
dotable1 <- print(table1, quote=TRUE, noSpaces=TRUE)
"Stratified by day_sleep"
"" "0" "1" "p" "test"
"n" "4339" "1517" "" ""
"RIAGENDR = 2 (%)" "2167 (49.9)" "849 (56.0)" "<0.001" ""
"ageCat_18 (%)" "" "" "0.001" ""
" 18-39" "1405 (32.4)" "569 (37.5)" "" ""
" 40-59" "1322 (30.5)" "410 (27.0)" "" ""
" 60+" "1612 (37.2)" "538 (35.5)" "" ""
"INDFMPIR (mean (SD))" "2.60 (1.62)" "2.31 (1.57)" "<0.001" ""
"SMQ681 = 2 (%)" "3015 (79.5)" "1013 (75.5)" "0.003" ""
"raceEthCat (%)" "" "" "<0.001" ""
" NH White" "1342 (30.9)" "690 (45.5)" "" ""
" NH Black" "1033 (23.8)" "310 (20.4)" "" ""
" NH Asian" "729 (16.8)" "120 (7.9)" "" ""
" Hispanic" "1031 (23.8)" "304 (20.0)" "" ""
" NH Other/Multiple" "204 (4.7)" "93 (6.1)" "" ""
"activity = 1 (%)" "2942 (67.9)" "1006 (66.4)" "0.325" ""
"hi_caffeine = 1 (%)" "139 (4.4)" "81 (7.0)" "0.001" ""
"BMI_cat (%)" "" "" "<0.001" ""
" underweight" "76 (1.9)" "23 (1.6)" "" ""
" normal" "1074 (26.7)" "298 (21.1)" "" ""
" overweight" "1333 (33.2)" "394 (27.9)" "" ""
" obese" "1538 (38.2)" "698 (49.4)" "" ""
"heavy_drink2 = 1 (%)" "1180 (31.2)" "503 (37.6)" "<0.001" ""
"depress_cat (%)" "" "" "<0.001" ""
" nodep" "3093 (82.5)" "679 (51.4)" "" ""
" mild_dep" "456 (12.2)" "381 (28.8)" "" ""
" mod_dep" "134 (3.6)" "158 (12.0)" "" ""
" mod_sev_dep" "48 (1.3)" "76 (5.8)" "" ""
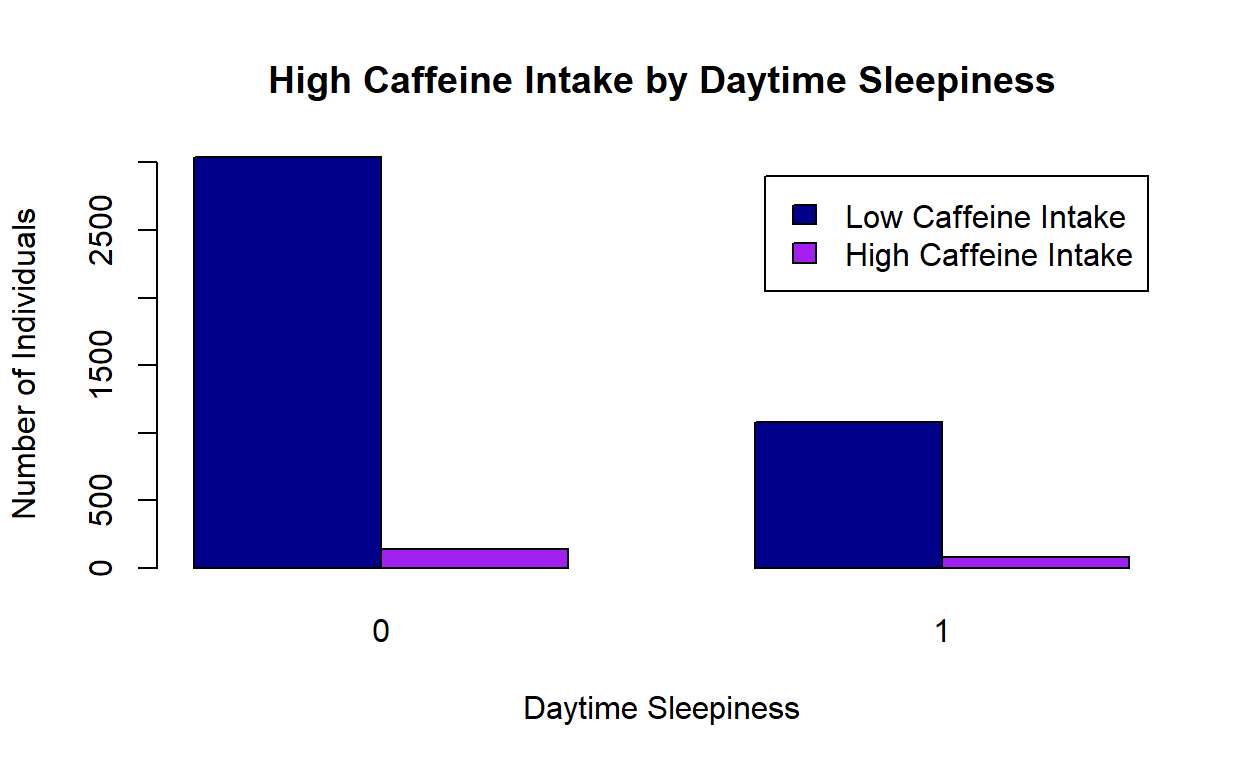
" sev_dep" "16 (0.4)" "27 (2.0)" "" "" Figure 1: Caffeine intake and Daytime Sleepiness
#png("Barplot Caffeine.png")
counts <- table(unweighted_data$hi_caffeine, unweighted_data$day_sleep)
barplot(counts, main="High Caffeine Intake by Daytime Sleepiness",
ylab = "Number of Individuals",
xlab="Daytime Sleepiness", col=c("darkblue","purple"),
legend = c("Low Caffeine Intake", "High Caffeine Intake"), beside=TRUE)
#dev.off()
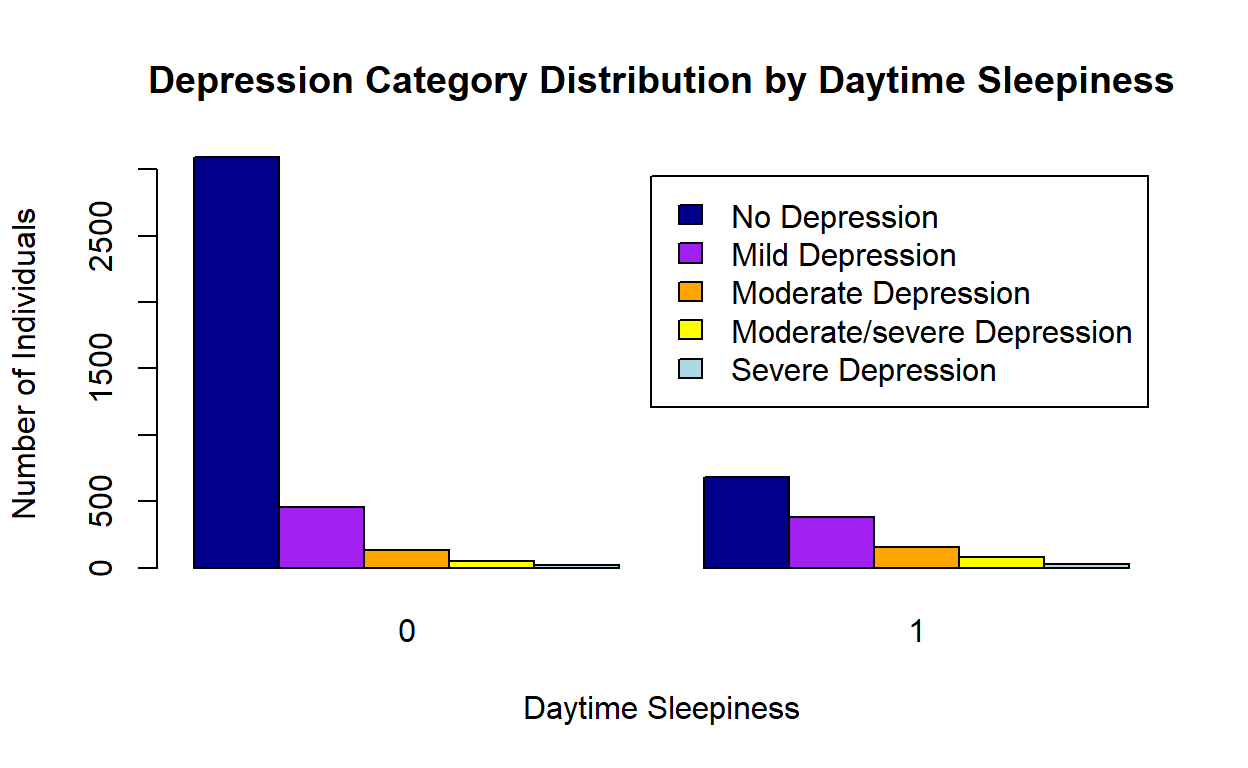
Figure 2: Dperession and Daytime Sleepiness
#png("Barplot Depression.png")
counts <- table(unweighted_data$depress_cat, unweighted_data$day_sleep)
barplot(counts, main="Depression Category Distribution by Daytime Sleepiness",
ylab = "Number of Individuals",
xlab="Daytime Sleepiness", col=c("darkblue","purple","orange","yellow","lightblue"),
legend = c("No Depression", "Mild Depression", "Moderate Depression", "Moderate/severe Depression", "Severe Depression"), beside=TRUE)
#dev.off()
Statistical Methods
Let’s develop a pipeline for our statistical analyses!
- Part a: Scatterplot matrices
- Part b: Fit weighted and unweighted SLRs
- Part c: Fit initial weighted and unweighted MLR model using all predictors
- Part d: Best subset model selection and human-selected model
- Part e. Compare model AICs and goodness of fit
- Part f: Check model: Analysis of Residuals
- Part f-1: Plot person residuals -vs- predicted values
- Part f-2: Boxplot and list outlier studentized residuals
- Part g: Check model: leverage boxplots
- Part h: Check model: influence
- Part h-1: Make boxplot and list outliers for influence
- Part h-2: Leverage -vs- residual squared (L-R) plot
- Part i: Sensitivity analysis: Re-fit without influential points
- Part j: Check for multi-collinearity using variance inflation factors
Part a: Scatterplot matrices
Using the ggpairs() function, which is nice for getting a quick scatterplot matrix plot
We must first created an unweighted dataset of those >=18.
Then we will make two separate scatterplot matrices. We must do this because if we make one matrix, it will be way too large and difficult to read. First we will make one of personal characteristics, and second, we will make one of lifestyle/behavioral characteristics.
unweighted_data <- filter(data, RIDAGEYR >=18)
#pdf("scatterplot_matrices_person.pdf")
unweighted_data %>%
dplyr::select(RIAGENDR, RIDAGEYR, INDFMPIR,depress_score,BMXBMI) %>%
pairs(upper.panel=NULL)
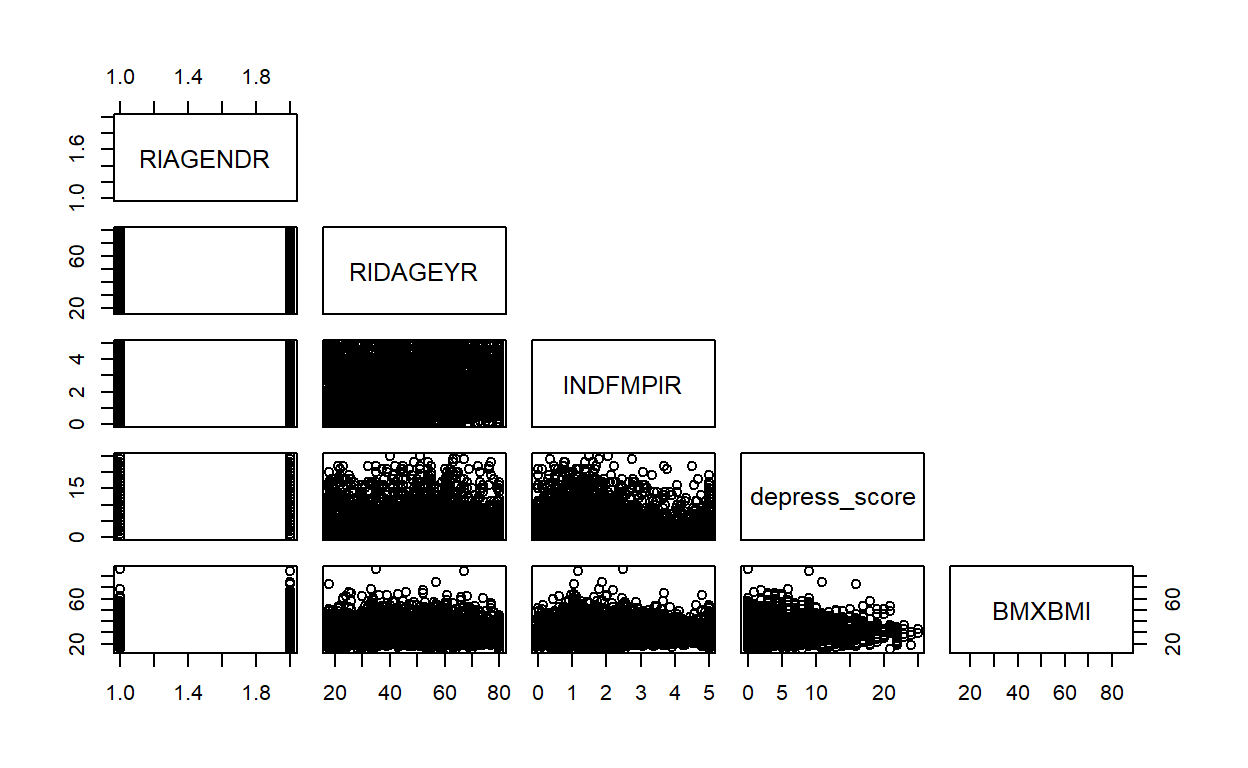
#dev.off()
#pdf("scatterplot_matrices_behavior.pdf")
unweighted_data %>%
dplyr::select(avg_mg_caffeine,SMQ681,ALQ130,activity) %>%
pairs(upper.panel=NULL)
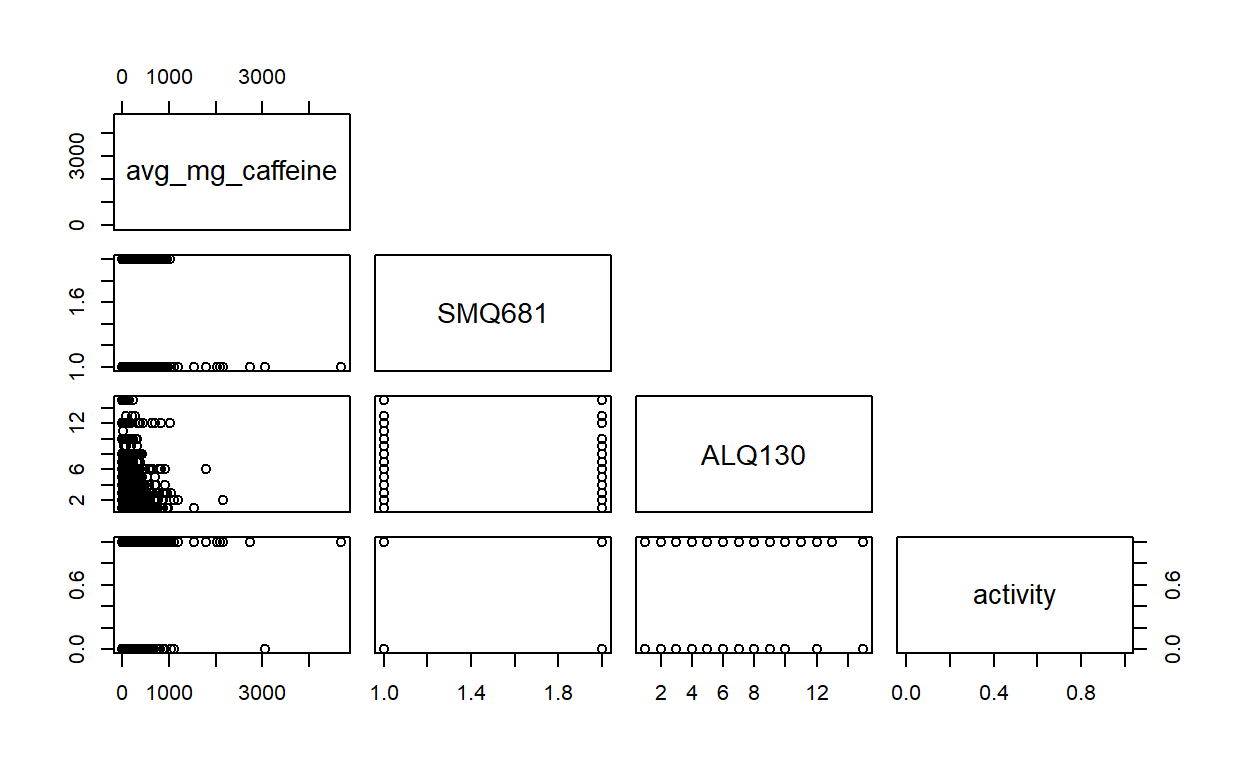
#dev.off()
There is no clear correlation between X’s.
Part b: Fit weighted and unweighted SLRs
Create a survey weight object
Fit the weighted univariate models and store the results. We are calculating the change in log prevalence odds of daytime sleepiness, our outcome, among levels of the “exposures”. Our exposures of interest are sex, age groups, income, smoking, race/ethnicity, any activity, high caffeine intake, BMI categories, heavy drinking, and ordinal depression scores. Log-binomial regression is used to estimate crude associations.
model_1w <- svyglm(day_sleep~RIAGENDR, design=NHANES, family=quasibinomial(link="log"))
model_2w <- svyglm(day_sleep~ageCat_18, design=NHANES, family=quasibinomial(link="log"))
model_3w <- svyglm(day_sleep~INDFMPIR, design=NHANES, family=quasibinomial(link="log"))
model_4w <- svyglm(day_sleep~SMQ681, design=NHANES, family=quasibinomial(link="log"))
model_5w <- svyglm(day_sleep~raceEthCat, design=NHANES, family=quasibinomial(link="log"))
model_6w <- svyglm(day_sleep~activity, design=NHANES, family=quasibinomial(link="log"))
model_7w <- svyglm(day_sleep~hi_caffeine, design=NHANES_MEC, family=quasibinomial(link="log"))
model_8w <- svyglm(day_sleep~BMI_cat, design=NHANES_MEC, family=quasibinomial(link="log"))
model_9w <- svyglm(day_sleep~heavy_drink2, design=NHANES, family=quasibinomial(link="log"))
model_10w <- svyglm(day_sleep~depress_cat, design=NHANES, family=quasibinomial(link="log"))
#exponentiated coefficients
exp(model_1w$coefficients)
(Intercept) RIAGENDR
0.2048742 1.2206388 exp(model_2w$coefficients)
(Intercept) ageCat_1840-59 ageCat_1860+
0.3183220 0.7924395 0.8044204 exp(model_3w$coefficients)
(Intercept) INDFMPIR
0.3767510 0.9118087 exp(model_4w$coefficients)
(Intercept) SMQ681
0.4012766 0.8151968 exp(model_5w$coefficients)
(Intercept) raceEthCatNH Black
0.3024167 0.8091614
raceEthCatNH Asian raceEthCatHispanic
0.4615732 0.7857788
raceEthCatNH Other/Multiple
1.2061075 exp(model_6w$coefficients)
(Intercept) activity
0.2791679 0.9971760 exp(model_7w$coefficients)
(Intercept) hi_caffeine
0.2679387 1.4338962 exp(model_8w$coefficients)
(Intercept) BMI_catunderweight BMI_catoverweight
0.2221463 1.2402763 1.0529336
BMI_catobese
1.5503832 exp(model_9w$coefficients)
(Intercept) heavy_drink2
0.2525171 1.2794627 exp(model_10w$coefficients)
(Intercept) depress_cat.L depress_cat.Q depress_cat.C depress_cat^4
0.4645206 2.2088022 0.5980783 1.2557422 0.9903052 # p-values
summary(model_1w)
Call:
svyglm(formula = day_sleep ~ RIAGENDR, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.58536 0.15227 -10.412 5.65e-08 ***
RIAGENDR 0.19937 0.08474 2.353 0.0338 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.000171)
Number of Fisher Scoring iterations: 6summary(model_2w)
Call:
svyglm(formula = day_sleep ~ ageCat_18, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.14469 0.05047 -22.680 7.73e-12 ***
ageCat_1840-59 -0.23264 0.06337 -3.671 0.00282 **
ageCat_1860+ -0.21763 0.07092 -3.069 0.00897 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.000171)
Number of Fisher Scoring iterations: 6summary(model_3w)
Call:
svyglm(formula = day_sleep ~ INDFMPIR, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.97617 0.08189 -11.920 1.02e-08 ***
INDFMPIR -0.09233 0.01919 -4.811 0.000277 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.026985)
Number of Fisher Scoring iterations: 6summary(model_4w)
Call:
svyglm(formula = day_sleep ~ SMQ681, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.91310 0.12122 -7.532 2.74e-06 ***
SMQ681 -0.20433 0.05779 -3.535 0.00329 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.0229)
Number of Fisher Scoring iterations: 6summary(model_5w)
Call:
svyglm(formula = day_sleep ~ raceEthCat, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.19595 0.04884 -24.490 6.03e-11 ***
raceEthCatNH Black -0.21176 0.07694 -2.752 0.0188 *
raceEthCatNH Asian -0.77311 0.09487 -8.149 5.48e-06 ***
raceEthCatHispanic -0.24108 0.10810 -2.230 0.0475 *
raceEthCatNH Other/Multiple 0.18740 0.13200 1.420 0.1834
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.000171)
Number of Fisher Scoring iterations: 6summary(model_6w)
Call:
svyglm(formula = day_sleep ~ activity, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.275942 0.059430 -21.470 4.1e-12 ***
activity -0.002828 0.068327 -0.041 0.968
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.000872)
Number of Fisher Scoring iterations: 6summary(model_7w)
Call:
svyglm(formula = day_sleep ~ hi_caffeine, design = NHANES_MEC,
family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all_MEC, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.31700 0.03985 -33.050 1.09e-14 ***
hi_caffeine 0.36040 0.12757 2.825 0.0135 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.104844)
Number of Fisher Scoring iterations: 6summary(model_8w)
Call:
svyglm(formula = day_sleep ~ BMI_cat, design = NHANES_MEC, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all_MEC, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.50442 0.07922 -18.991 2.55e-10 ***
BMI_catunderweight 0.21533 0.28243 0.762 0.460528
BMI_catoverweight 0.05158 0.13810 0.374 0.715285
BMI_catobese 0.43850 0.10153 4.319 0.000998 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.064164)
Number of Fisher Scoring iterations: 6summary(model_9w)
Call:
svyglm(formula = day_sleep ~ heavy_drink2, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.37628 0.06028 -22.830 1.78e-12 ***
heavy_drink2 0.24644 0.05956 4.138 0.00101 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.022591)
Number of Fisher Scoring iterations: 6summary(model_10w)
Call:
svyglm(formula = day_sleep ~ depress_cat, design = NHANES, family = quasibinomial(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.766749 0.059637 -12.857 5.71e-08 ***
depress_cat.L 0.792450 0.105804 7.490 1.22e-05 ***
depress_cat.Q -0.514034 0.093152 -5.518 0.000181 ***
depress_cat.C 0.227727 0.075092 3.033 0.011395 *
depress_cat^4 -0.009742 0.075368 -0.129 0.899485
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 1.026629)
Number of Fisher Scoring iterations: 6 2.5 % 97.5 %
(Intercept) 0.1477932 0.2840011
RIAGENDR 1.0177826 1.4639265 2.5 % 97.5 %
(Intercept) 0.2854385 0.3549939
ageCat_1840-59 0.6910498 0.9087050
ageCat_1860+ 0.6901471 0.9376148 2.5 % 97.5 %
(Intercept) 0.3160633 0.4490912
INDFMPIR 0.8750411 0.9501211 2.5 % 97.5 %
(Intercept) 0.3094055 0.5204269
SMQ681 0.7201610 0.9227741 2.5 % 97.5 %
(Intercept) 0.2715973 0.3367333
raceEthCatNH Black 0.6831119 0.9584698
raceEthCatNH Asian 0.3745883 0.5687572
raceEthCatHispanic 0.6193948 0.9968574
raceEthCatNH Other/Multiple 0.9020059 1.6127337 2.5 % 97.5 %
(Intercept) 0.2457586 0.317119
activity 0.8612465 1.154559 2.5 % 97.5 %
(Intercept) 0.2459903 0.2918454
hi_caffeine 1.0906713 1.8851310 2.5 % 97.5 %
(Intercept) 0.1869307 0.2639961
BMI_catunderweight 0.6702992 2.2949234
BMI_catoverweight 0.7793414 1.4225720
BMI_catobese 1.2427144 1.9342241 2.5 % 97.5 %
(Intercept) 0.2218905 0.2873711
heavy_drink2 1.1260268 1.4538061 2.5 % 97.5 %
(Intercept) 0.4073797 0.5296763
depress_cat.L 1.7499334 2.7879959
depress_cat.Q 0.4872101 0.7341754
depress_cat.C 1.0644425 1.4814219
depress_cat^4 0.8389312 1.1689926Let’s also look at the univariate associations in unweighted models. We expect a change in the standard errors. It will not be as representative of the US population. We will store the results and diplay them in a table in the results section.
# fit the unweighted models and store the results
model_1u <- glm(day_sleep~RIAGENDR, family=binomial(link="log"), data = unweighted_data)
model_2u <- glm(day_sleep~ageCat_18, family=binomial(link="log"), data = unweighted_data)
model_3u <- glm(day_sleep~INDFMPIR, family=binomial(link="log"), data = unweighted_data)
model_4u <- glm(day_sleep~SMQ681, family=binomial(link="log"), data = unweighted_data)
model_5u <- glm(day_sleep~raceEthCat, family=binomial(link="log"), data = unweighted_data)
model_6u <- glm(day_sleep~activity, family=binomial(link="log"), data = unweighted_data)
model_7u <- glm(day_sleep~hi_caffeine, family=binomial(link="log"), data = unweighted_data)
model_8u <- glm(day_sleep~BMI_cat, family=binomial(link="log"), data = unweighted_data)
model_9u <- glm(day_sleep~heavy_drink2, family=binomial(link="log"), data = unweighted_data)
model_10u <- glm(day_sleep~depress_cat, family=binomial(link="log"), data = unweighted_data)
Part c: Fit initial MLR using all predictors
Multivariable Poisson regression with robust standard errors will be used to estimate adjusted prevalence ratios. Unweighted multivariable candidate models were selected in 4 ways:
- Including all predictors
- Best subset selection
- a-priori selection based on literature and common knowledge
- Combination of a priori and best-subset
First, lets run the models with every predictor
Note: logit models failed to converge. Use poisson model. From the svy package: svyglm always returns ‘model-robust’ standard errors; the Horvitz-Thompson-type standard errors used everywhere in the survey package are a generalisation of the model-robust ‘sandwich’ estimators. In particular, a quasi-Poisson svyglm will return correct standard errors for relative risk regression models.
Using Exam weights (recommended):
MLR_1 <- svyglm(day_sleep~RIAGENDR+ INDFMPIR + SMQ681 + ageCat_18+
+ raceEthCat + activity + hi_caffeine + BMI_cat +
heavy_drink2 + depress_cat, design=NHANES_MEC,
family=quasipoisson(link="log"))
summary(MLR_1, df.resid = degf(NHANES_MEC))
Call:
svyglm(formula = day_sleep ~ RIAGENDR + INDFMPIR + SMQ681 + ageCat_18 +
+raceEthCat + activity + hi_caffeine + BMI_cat + heavy_drink2 +
depress_cat, design = NHANES_MEC, family = quasipoisson(link = "log"))
Survey design:
subset(NHANES_all_MEC, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.082160 0.233512 -4.634 0.000324 ***
RIAGENDR 0.121471 0.078823 1.541 0.144130
INDFMPIR -0.052522 0.019994 -2.627 0.019049 *
SMQ681 0.095709 0.068990 1.387 0.185622
ageCat_1840-59 -0.226165 0.095069 -2.379 0.031076 *
ageCat_1860+ -0.238507 0.081341 -2.932 0.010300 *
raceEthCatNH Black -0.238056 0.105131 -2.264 0.038800 *
raceEthCatNH Asian -0.557554 0.173805 -3.208 0.005868 **
raceEthCatHispanic -0.307914 0.099593 -3.092 0.007442 **
raceEthCatNH Other/Multiple 0.064766 0.159042 0.407 0.689595
activity 0.026327 0.057780 0.456 0.655168
hi_caffeine 0.226425 0.095594 2.369 0.031709 *
BMI_catunderweight -0.062413 0.362150 -0.172 0.865473
BMI_catoverweight 0.105170 0.160207 0.656 0.521471
BMI_catobese 0.380563 0.106197 3.584 0.002716 **
heavy_drink2 0.058645 0.083379 0.703 0.492609
depress_cat.L 0.643917 0.102021 6.312 1.39e-05 ***
depress_cat.Q -0.426273 0.084199 -5.063 0.000140 ***
depress_cat.C 0.239641 0.093666 2.558 0.021828 *
depress_cat^4 -0.005434 0.075550 -0.072 0.943615
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Zero or negative residual df; p-values not defined
(Dispersion parameter for quasipoisson family taken to be 0.8208122)
Number of Fisher Scoring iterations: 6#linearHypothesis(MLR_1, "ageCat_1818-39=ageCat_1840-59")
#linearHypothesis(MLR_1, "ageCat_1818-39=ageCat_1860+")
exp(MLR_1$coefficients)
(Intercept) RIAGENDR
0.3388629 1.1291569
INDFMPIR SMQ681
0.9488333 1.1004391
ageCat_1840-59 ageCat_1860+
0.7975861 0.7878033
raceEthCatNH Black raceEthCatNH Asian
0.7881582 0.5726078
raceEthCatHispanic raceEthCatNH Other/Multiple
0.7349785 1.0669093
activity hi_caffeine
1.0266769 1.2541089
BMI_catunderweight BMI_catoverweight
0.9394944 1.1108992
BMI_catobese heavy_drink2
1.4631086 1.0603987
depress_cat.L depress_cat.Q
1.9039230 0.6529379
depress_cat.C depress_cat^4
1.2707934 0.9945811 Using Interview weights
MLR_2 <- svyglm(day_sleep~RIAGENDR + ageCat_18 + INDFMPIR + SMQ681
+ raceEthCat + activity + hi_caffeine + BMI_cat +
heavy_drink2 + depress_cat, design=NHANES,
family=quasipoisson(link="log"))
summary(MLR_2, df.resid = degf(NHANES))
Call:
svyglm(formula = day_sleep ~ RIAGENDR + ageCat_18 + INDFMPIR +
SMQ681 + raceEthCat + activity + hi_caffeine + BMI_cat +
heavy_drink2 + depress_cat, design = NHANES, family = quasipoisson(link = "log"))
Survey design:
subset(NHANES_all, inAnalysis == 1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.089417 0.237501 -4.587 0.000356 ***
RIAGENDR 0.125684 0.080332 1.565 0.138535
ageCat_1840-59 -0.226016 0.093995 -2.405 0.029561 *
ageCat_1860+ -0.252454 0.080819 -3.124 0.006972 **
INDFMPIR -0.052001 0.019399 -2.681 0.017113 *
SMQ681 0.093046 0.069257 1.343 0.199087
raceEthCatNH Black -0.239878 0.105846 -2.266 0.038658 *
raceEthCatNH Asian -0.556917 0.176800 -3.150 0.006607 **
raceEthCatHispanic -0.306654 0.098127 -3.125 0.006952 **
raceEthCatNH Other/Multiple 0.065960 0.164823 0.400 0.694660
activity 0.039479 0.059561 0.663 0.517487
hi_caffeine 0.235958 0.094373 2.500 0.024492 *
BMI_catunderweight -0.097781 0.377249 -0.259 0.799009
BMI_catoverweight 0.107206 0.162556 0.660 0.519570
BMI_catobese 0.380365 0.107844 3.527 0.003050 **
heavy_drink2 0.052873 0.082232 0.643 0.529948
depress_cat.L 0.643541 0.105453 6.103 2.02e-05 ***
depress_cat.Q -0.422803 0.083392 -5.070 0.000138 ***
depress_cat.C 0.250825 0.089710 2.796 0.013570 *
depress_cat^4 0.001431 0.076402 0.019 0.985299
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Zero or negative residual df; p-values not defined
(Dispersion parameter for quasipoisson family taken to be 0.7764147)
Number of Fisher Scoring iterations: 6exp(MLR_2$coefficients)
(Intercept) RIAGENDR
0.3364125 1.1339234
ageCat_1840-59 ageCat_1860+
0.7977057 0.7768921
INDFMPIR SMQ681
0.9493281 1.0975126
raceEthCatNH Black raceEthCatNH Asian
0.7867238 0.5729726
raceEthCatHispanic raceEthCatNH Other/Multiple
0.7359049 1.0681840
activity hi_caffeine
1.0402691 1.2661215
BMI_catunderweight BMI_catoverweight
0.9068478 1.1131640
BMI_catobese heavy_drink2
1.4628178 1.0542955
depress_cat.L depress_cat.Q
1.9032081 0.6552077
depress_cat.C depress_cat^4
1.2850850 1.0014325 Un-weighted
MLR_3 <- glm(day_sleep~RIAGENDR + ageCat_18 + INDFMPIR + SMQ681
+ raceEthCat + activity + hi_caffeine + BMI_cat +
heavy_drink2 + depress_cat, family=poisson(link="log"), data = unweighted_data)
summary(MLR_3)
Call:
glm(formula = day_sleep ~ RIAGENDR + ageCat_18 + INDFMPIR + SMQ681 +
raceEthCat + activity + hi_caffeine + BMI_cat + heavy_drink2 +
depress_cat, family = poisson(link = "log"), data = unweighted_data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3717 -0.6854 -0.5868 0.3796 1.7553
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.80381 0.20016 -4.016 5.92e-05 ***
RIAGENDR 0.06662 0.06524 1.021 0.30718
ageCat_1840-59 -0.18448 0.08036 -2.296 0.02169 *
ageCat_1860+ -0.19778 0.08158 -2.424 0.01534 *
INDFMPIR -0.03071 0.02143 -1.433 0.15184
SMQ681 0.10030 0.08124 1.235 0.21696
raceEthCatNH Black -0.34815 0.08526 -4.083 4.44e-05 ***
raceEthCatNH Asian -0.64845 0.13840 -4.686 2.79e-06 ***
raceEthCatHispanic -0.37725 0.08883 -4.247 2.17e-05 ***
raceEthCatNH Other/Multiple -0.13584 0.13158 -1.032 0.30192
activity -0.06755 0.07090 -0.953 0.34068
hi_caffeine 0.11217 0.12508 0.897 0.36983
BMI_catunderweight -0.26905 0.28795 -0.934 0.35012
BMI_catoverweight 0.08017 0.09485 0.845 0.39798
BMI_catobese 0.23308 0.08521 2.735 0.00623 **
heavy_drink2 0.02428 0.07038 0.345 0.73014
depress_cat.L 0.72063 0.15763 4.572 4.84e-06 ***
depress_cat.Q -0.43440 0.14050 -3.092 0.00199 **
depress_cat.C 0.21783 0.12248 1.779 0.07531 .
depress_cat^4 -0.05760 0.10252 -0.562 0.57419
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2612.4 on 3678 degrees of freedom
Residual deviance: 2320.8 on 3659 degrees of freedom
(2177 observations deleted due to missingness)
AIC: 4384.8
Number of Fisher Scoring iterations: 6coeftest(MLR_3, vcov = sandwich)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.803810 0.155923 -5.1552 2.534e-07
RIAGENDR 0.066625 0.052285 1.2743 0.202572
ageCat_1840-59 -0.184479 0.063186 -2.9196 0.003504
ageCat_1860+ -0.197776 0.065378 -3.0251 0.002485
INDFMPIR -0.030711 0.017555 -1.7494 0.080213
SMQ681 0.100302 0.064105 1.5647 0.117662
raceEthCatNH Black -0.348150 0.069915 -4.9796 6.370e-07
raceEthCatNH Asian -0.648454 0.123021 -5.2711 1.356e-07
raceEthCatHispanic -0.377252 0.071291 -5.2917 1.212e-07
raceEthCatNH Other/Multiple -0.135836 0.098084 -1.3849 0.166087
activity -0.067554 0.056518 -1.1952 0.231990
hi_caffeine 0.112169 0.094040 1.1928 0.232956
BMI_catunderweight -0.269051 0.228246 -1.1788 0.238488
BMI_catoverweight 0.080168 0.079409 1.0096 0.312710
BMI_catobese 0.233082 0.070999 3.2829 0.001027
heavy_drink2 0.024277 0.056023 0.4333 0.664765
depress_cat.L 0.720634 0.097246 7.4104 1.259e-13
depress_cat.Q -0.434399 0.086629 -5.0145 5.318e-07
depress_cat.C 0.217833 0.075467 2.8864 0.003896
depress_cat^4 -0.057602 0.065414 -0.8806 0.378544
(Intercept) ***
RIAGENDR
ageCat_1840-59 **
ageCat_1860+ **
INDFMPIR .
SMQ681
raceEthCatNH Black ***
raceEthCatNH Asian ***
raceEthCatHispanic ***
raceEthCatNH Other/Multiple
activity
hi_caffeine
BMI_catunderweight
BMI_catoverweight
BMI_catobese **
heavy_drink2
depress_cat.L ***
depress_cat.Q ***
depress_cat.C **
depress_cat^4
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1exp(MLR_3$coefficients)
(Intercept) RIAGENDR
0.4476202 1.0688942
ageCat_1840-59 ageCat_1860+
0.8315377 0.8205536
INDFMPIR SMQ681
0.9697560 1.1055052
raceEthCatNH Black raceEthCatNH Asian
0.7059933 0.5228535
raceEthCatHispanic raceEthCatNH Other/Multiple
0.6857430 0.8729861
activity hi_caffeine
0.9346777 1.1187019
BMI_catunderweight BMI_catoverweight
0.7641043 1.0834689
BMI_catobese heavy_drink2
1.2624850 1.0245741
depress_cat.L depress_cat.Q
2.0557369 0.6476537
depress_cat.C depress_cat^4
1.2433790 0.9440252 The unweighted regression results are qualitatively the same as the weighted regression results. I I also am not able to easily perform regression diagnostics with the survey weighted glm, so I will proceed with the unweighted model 3 for simplicity. This is reasonable, since we are trying to observe risk factors to daytime sleepiness in our sample and are not trying to predict prevalence of these risk factors in the United States population.
Part d: selection of best model using AIC and a priori
Next, we will run our best subset AI model to select the most parsimonious predictors
We will also attempt best-subset model selection to ensure that we are not missing any potentially relevant variables in our a-priori models.
analytic_data <- na.omit(unweighted_data)
# can do this all at once with step function when done by AIC
model_0 <- glm(day_sleep ~ 1, data = analytic_data, family = poisson(link = "log")) # start with null model
mod_final <- step(model_0, scope = ~ . + RIAGENDR + ageCat_18 + INDFMPIR-1 + SMQ681
+ activity + hi_caffeine + BMI_cat + raceEthCat +
heavy_drink2 + depress_cat, family=poisson(link="log"),
data = analytic_data, direction = "forward", na.rm = TRUE) # add terms one at a time using AIC
Start: AIC=2514.33
day_sleep ~ 1
Df Deviance AIC
+ depress_cat 4 1198.9 2450.9
+ raceEthCat 4 1256.2 2508.2
+ INDFMPIR 1 1262.8 2508.8
+ BMI_cat 3 1262.0 2512.0
+ hi_caffeine 1 1267.4 2513.4
<none> 1270.3 2514.3
+ RIAGENDR 1 1269.2 2515.2
+ ageCat_18 2 1267.8 2515.8
+ heavy_drink2 1 1269.8 2515.8
+ SMQ681 1 1269.9 2515.9
+ activity 1 1270.2 2516.2
Step: AIC=2450.89
day_sleep ~ depress_cat
Df Deviance AIC
+ raceEthCat 4 1187.4 2447.4
<none> 1198.9 2450.9
+ INDFMPIR 1 1197.1 2451.1
+ hi_caffeine 1 1197.8 2451.8
+ ageCat_18 2 1195.8 2451.8
+ RIAGENDR 1 1198.4 2452.4
+ BMI_cat 3 1194.5 2452.5
+ activity 1 1198.5 2452.5
+ SMQ681 1 1198.7 2452.7
+ heavy_drink2 1 1198.9 2452.9
Step: AIC=2447.4
day_sleep ~ depress_cat + raceEthCat
Df Deviance AIC
+ ageCat_18 2 1183.2 2447.2
+ INDFMPIR 1 1185.3 2447.3
<none> 1187.4 2447.4
+ SMQ681 1 1186.8 2448.8
+ RIAGENDR 1 1187.1 2449.1
+ activity 1 1187.1 2449.1
+ hi_caffeine 1 1187.1 2449.1
+ heavy_drink2 1 1187.4 2449.4
+ BMI_cat 3 1183.4 2449.4
Step: AIC=2447.2
day_sleep ~ depress_cat + raceEthCat + ageCat_18
Df Deviance AIC
<none> 1183.2 2447.2
+ INDFMPIR 1 1181.7 2447.7
+ SMQ681 1 1182.0 2448.0
+ BMI_cat 3 1178.4 2448.4
+ hi_caffeine 1 1182.7 2448.7
+ heavy_drink2 1 1183.0 2448.9
+ RIAGENDR 1 1183.0 2449.0
+ activity 1 1183.2 2449.2coeftest(mod_final, vcov. = sandwich)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.482284 0.063935 -7.5433 4.581e-14
depress_cat.L 0.576384 0.129384 4.4548 8.396e-06
depress_cat.Q -0.392328 0.115405 -3.3996 0.0006749
depress_cat.C 0.042799 0.092111 0.4646 0.6421856
depress_cat^4 -0.041453 0.074945 -0.5531 0.5801898
raceEthCatNH Black -0.232862 0.083771 -2.7798 0.0054400
raceEthCatNH Asian -0.448282 0.149246 -3.0036 0.0026677
raceEthCatHispanic -0.277537 0.084456 -3.2862 0.0010156
raceEthCatNH Other/Multiple -0.150954 0.115582 -1.3060 0.1915424
ageCat_1840-59 -0.115274 0.071351 -1.6156 0.1061843
ageCat_1860+ -0.204843 0.079876 -2.5645 0.0103322
(Intercept) ***
depress_cat.L ***
depress_cat.Q ***
depress_cat.C
depress_cat^4
raceEthCatNH Black **
raceEthCatNH Asian **
raceEthCatHispanic **
raceEthCatNH Other/Multiple
ageCat_1840-59
ageCat_1860+ *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(mod_final)
Call:
glm(formula = day_sleep ~ depress_cat + raceEthCat + ageCat_18,
family = poisson(link = "log"), data = analytic_data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2781 -0.7799 -0.6942 0.6298 1.3459
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.48228 0.09852 -4.895 9.81e-07 ***
depress_cat.L 0.57638 0.20265 2.844 0.00445 **
depress_cat.Q -0.39233 0.18092 -2.169 0.03012 *
depress_cat.C 0.04280 0.14962 0.286 0.77484
depress_cat^4 -0.04145 0.12182 -0.340 0.73365
raceEthCatNH Black -0.23286 0.10737 -2.169 0.03009 *
raceEthCatNH Asian -0.44828 0.17580 -2.550 0.01077 *
raceEthCatHispanic -0.27754 0.10892 -2.548 0.01083 *
raceEthCatNH Other/Multiple -0.15095 0.16024 -0.942 0.34617
ageCat_1840-59 -0.11527 0.09378 -1.229 0.21900
ageCat_1860+ -0.20484 0.10283 -1.992 0.04637 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1270.3 on 1726 degrees of freedom
Residual deviance: 1183.2 on 1716 degrees of freedom
AIC: 2447.2
Number of Fisher Scoring iterations: 5exp(mod_final$coefficients)
(Intercept) depress_cat.L
0.6173715 1.7795910
depress_cat.Q depress_cat.C
0.6754827 1.0437281
depress_cat^4 raceEthCatNH Black
0.9593946 0.7922631
raceEthCatNH Asian raceEthCatHispanic
0.6387248 0.7576473
raceEthCatNH Other/Multiple ageCat_1840-59
0.8598874 0.8911220
ageCat_1860+
0.8147754 We see the final model has depression category, race, and age as the most parsimonious predictors explaining daytime sleepiness in our sample
Now, let’s look at our a-priori models
Model using behavioral risk factors only (a priori)
mod_behav <- glm(day_sleep~SMQ681 + activity + hi_caffeine + heavy_drink2,
family=poisson(link="log"), data = unweighted_data)
#robust variance
coeftest(mod_behav, vcov = sandwich)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.161584 0.122919 -9.4500 < 2.2e-16 ***
SMQ681 -0.085705 0.061396 -1.3959 0.1627367
activity -0.109537 0.054449 -2.0117 0.0442484 *
hi_caffeine 0.320028 0.094668 3.3805 0.0007235 ***
heavy_drink2 0.149307 0.054189 2.7553 0.0058635 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#coefficents
exp(mod_behav$coefficients)
(Intercept) SMQ681 activity hi_caffeine heavy_drink2
0.3129899 0.9178654 0.8962488 1.3771665 1.1610298 Model combining a priori and best-subset selection
mod_final_behav <- glm(day_sleep~depress_cat + ageCat_18 + SMQ681 + activity + raceEthCat +
hi_caffeine + heavy_drink2, family=poisson(link="log"), data = unweighted_data)
summary(mod_final_behav)
Call:
glm(formula = day_sleep ~ depress_cat + ageCat_18 + SMQ681 +
activity + raceEthCat + hi_caffeine + heavy_drink2, family = poisson(link = "log"),
data = unweighted_data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3059 -0.6649 -0.5739 0.3749 1.7463
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.60500 0.15997 -3.782 0.000156 ***
depress_cat.L 0.83543 0.13796 6.056 1.40e-09 ***
depress_cat.Q -0.40609 0.12492 -3.251 0.001151 **
depress_cat.C 0.29800 0.11183 2.665 0.007706 **
depress_cat^4 -0.03835 0.09589 -0.400 0.689213
ageCat_1840-59 -0.18828 0.07594 -2.479 0.013167 *
ageCat_1860+ -0.21188 0.07645 -2.772 0.005579 **
SMQ681 0.10213 0.07482 1.365 0.172250
activity -0.09067 0.06641 -1.365 0.172142
raceEthCatNH Black -0.34672 0.08010 -4.328 1.50e-05 ***
raceEthCatNH Asian -0.78766 0.13358 -5.897 3.71e-09 ***
raceEthCatHispanic -0.36168 0.08289 -4.363 1.28e-05 ***
raceEthCatNH Other/Multiple -0.13766 0.12599 -1.093 0.274537
hi_caffeine 0.11937 0.12200 0.978 0.327873
heavy_drink2 0.03806 0.06676 0.570 0.568567
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2935.0 on 4164 degrees of freedom
Residual deviance: 2599.7 on 4150 degrees of freedom
(1691 observations deleted due to missingness)
AIC: 4847.7
Number of Fisher Scoring iterations: 6coeftest(mod_final_behav, vcov = sandwich)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.604997 0.121445 -4.9817 6.304e-07
depress_cat.L 0.835431 0.081969 10.1920 < 2.2e-16
depress_cat.Q -0.406091 0.075380 -5.3872 7.156e-08
depress_cat.C 0.297997 0.071108 4.1908 2.780e-05
depress_cat^4 -0.038350 0.063182 -0.6070 0.5438610
ageCat_1840-59 -0.188282 0.060499 -3.1122 0.0018573
ageCat_1860+ -0.211885 0.061448 -3.4482 0.0005643
SMQ681 0.102129 0.059907 1.7048 0.0882301
activity -0.090669 0.052991 -1.7110 0.0870746
raceEthCatNH Black -0.346716 0.065189 -5.3187 1.045e-07
raceEthCatNH Asian -0.787660 0.119233 -6.6061 3.946e-11
raceEthCatHispanic -0.361676 0.067043 -5.3947 6.863e-08
raceEthCatNH Other/Multiple -0.137664 0.096014 -1.4338 0.1516323
hi_caffeine 0.119369 0.092434 1.2914 0.1965662
heavy_drink2 0.038062 0.053537 0.7110 0.4771127
(Intercept) ***
depress_cat.L ***
depress_cat.Q ***
depress_cat.C ***
depress_cat^4
ageCat_1840-59 **
ageCat_1860+ ***
SMQ681 .
activity .
raceEthCatNH Black ***
raceEthCatNH Asian ***
raceEthCatHispanic ***
raceEthCatNH Other/Multiple
hi_caffeine
heavy_drink2
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Part e: AIC and Goodness of Fit (pearson’s chi-sq)
Now I will compare the fit of the models. I calculate deviance residuals since the models are poisson, not linear.
with(mod_final_behav, cbind(res.deviance = deviance, df = df.residual, p = pchisq(deviance, df.residual, lower.tail=FALSE)))
res.deviance df p
[1,] 2599.738 4150 1with(mod_final, cbind(res.deviance = deviance, df = df.residual,
p = pchisq(deviance, df.residual, lower.tail=FALSE)))
res.deviance df p
[1,] 1183.199 1716 1with(MLR_3, cbind(res.deviance = deviance, df = df.residual,
p = pchisq(deviance, df.residual, lower.tail=FALSE)))
res.deviance df p
[1,] 2320.764 3659 1I calculate the fit of the models using Aikake’s Information Criterion, a measure of parsimony and model goodness of fit:
There was some lost data in the best subset regression since there was some missingness. Therefore, the AIC is not as great as it seems when run on the full dataset. Let’s try the best subset model on the full data:
Mod_bestsub <- glm(day_sleep ~ ageCat_18 + depress_cat + raceEthCat, data = unweighted_data, family = poisson(link = "log"))
AIC(Mod_bestsub)
[1] 5802.821We see in the analyses above that the model with the best fit is the model including all covariates. However, since the epidemiologic question is seeking to understand which the behavioral risk factors may be the most impactful on daytime sleepiness, we will proceed with the model including all behavioral covariates (ever smoking, moderate/high physical activity, race, high caffeine consumption, and heavy drinking) plus the covariates identified in the best-subset model (age and depression).
Part f: Model diagnostics
Model diagnostics that we will perform include residual versus fitted plots, Q-Q plots, leverage boxplots, residual boxplots and influential point boxplots.
Part f-1: Plot studentized residual -vs- predicted values
Calculate predicted values and residuals in weighted data - model w/ all covariates
fit_dat <- as.data.frame(MLR_1$fitted.values)
pearson_res_w <- residuals(MLR_1, type = "pearson")
fit_dat <- cbind(fit_dat, pearson_res_w)
fit_dat %>%
ggplot(aes(x = MLR_1$fitted.values, y = pearson_res_w)) +
geom_point() +
geom_hline(yintercept = c(-2, 0, 2), col="red") +
geom_smooth(method = lm) +
labs(x = "Fitted values", y = "Pearson Residuals", title = "Residuals vs. Fitted values")
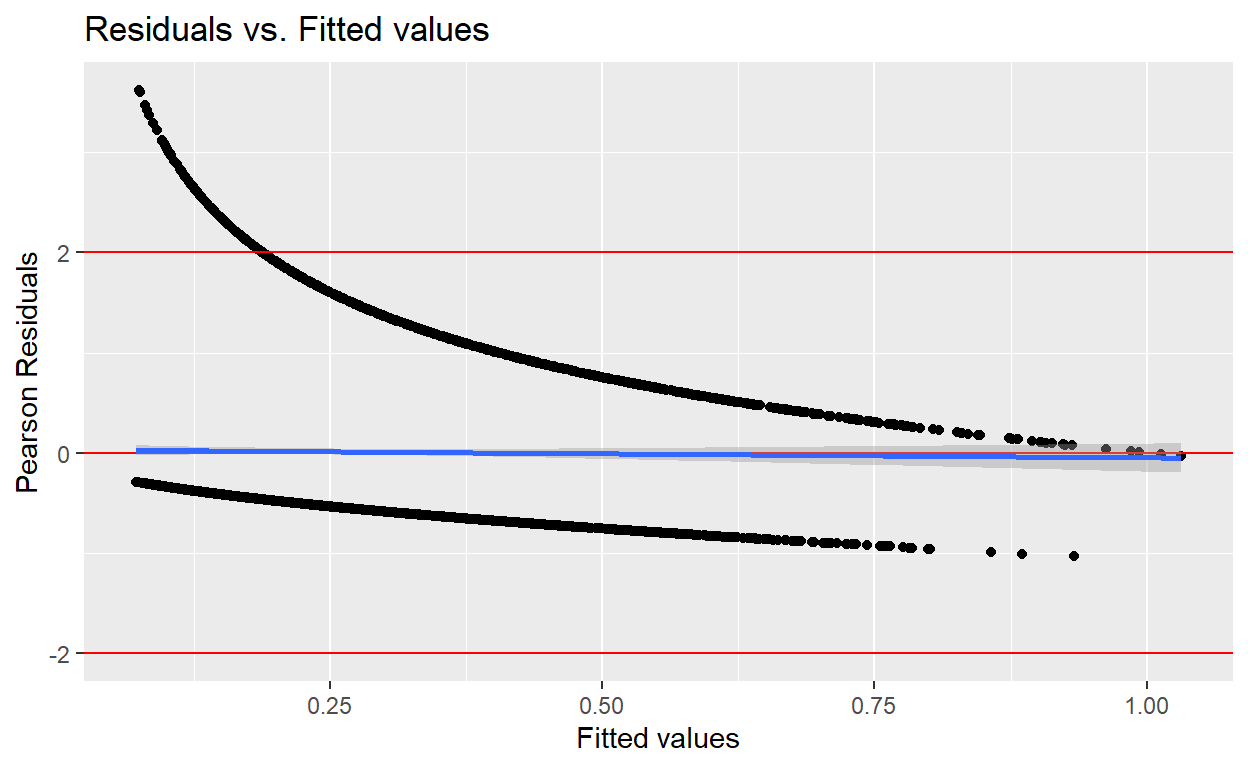
ggsave("pearson_resids_weighted.png", width = 6, height = 4, units = "in")
Calculate predicted values and residuals in unweighted data - model w/ all covariates
fit_dat2 <- as.data.frame(MLR_3$fitted.values)
pearson_res <- residuals(MLR_3, type = "pearson")
fit_dat2 <- cbind(fit_dat2, pearson_res)
fit_dat2 %>%
ggplot(aes(x = MLR_3$fitted.values, y = pearson_res)) +
geom_point() +
geom_hline(yintercept = c(-2, 0, 2), col="red") +
geom_smooth(method = lm) +
labs(x = "Fitted values", y = "Pearson Residuals", title = "Residuals vs. Fitted values")
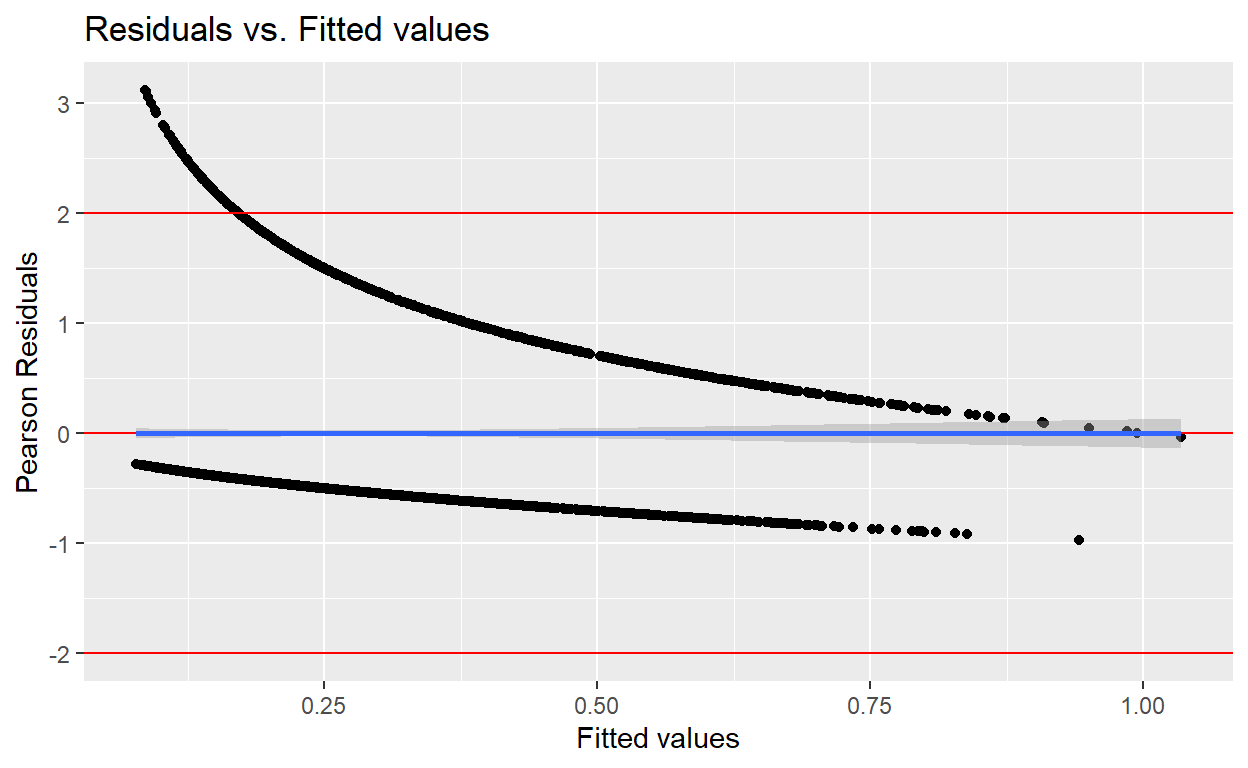
ggsave("pearson_resids_unweighted.png", width = 6, height = 4, units = "in")
The loess line is flat, which means there is no trend in the residuals. Equal variances/ linear assumption is met.
Calculate predicted values and residuals in unweighted final model
fit_dat_fin <- as.data.frame(mod_final_behav$fitted.values)
pearson_res_fin <- residuals(mod_final_behav, type = "pearson")
fit_dat_fin <- cbind(fit_dat_fin, pearson_res_fin)
fit_dat_fin %>%
ggplot(aes(x = mod_final_behav$fitted.values, y = pearson_res_fin)) +
geom_point() +
geom_hline(yintercept = c(-2, 0, 2), col="red") +
geom_smooth(method = lm) +
labs(x = "Fitted values", y = "Pearson Residuals", title = "Residuals vs. Fitted values")
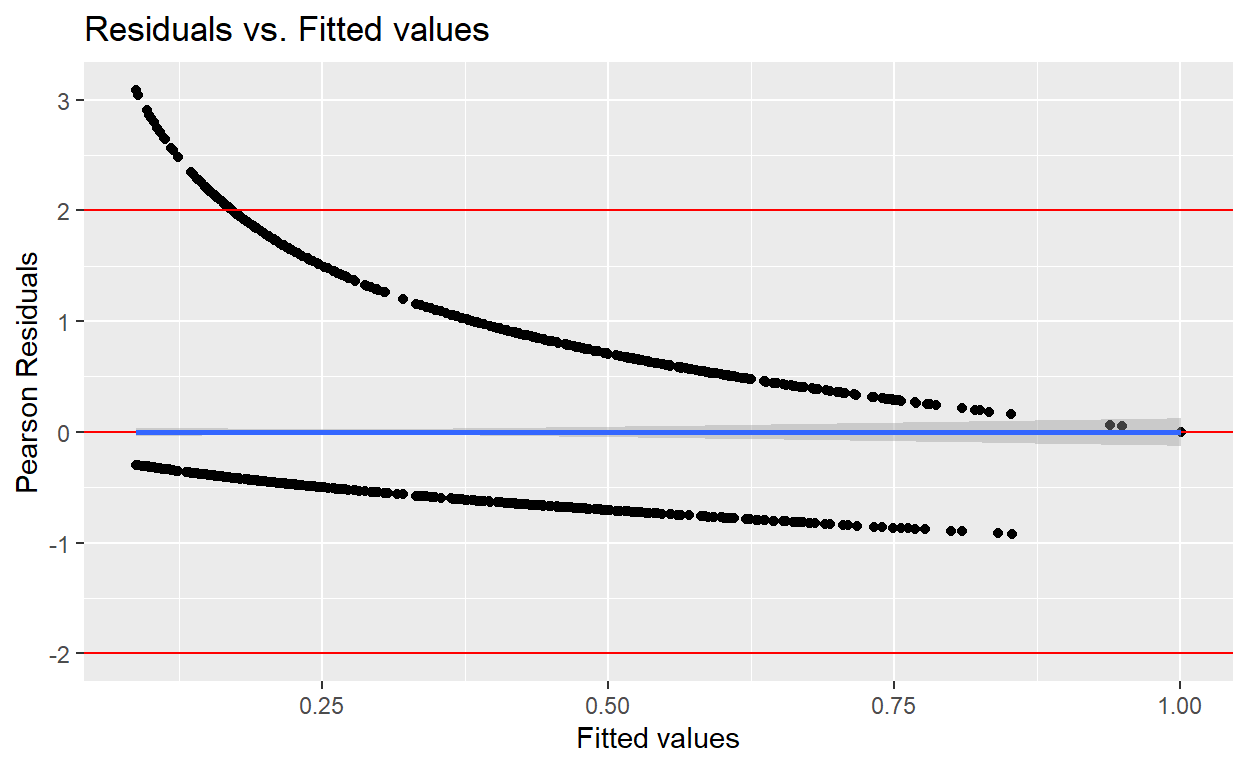
ggsave("pearson_resids_final_behave_model.png", width = 6, height = 4, units = "in")
Now, let’s create a Q-Q plot of deviance residuals for the final model and the model including all covariates
fit_dat_fin_apriori <- as.data.frame(mod_final_behav$fitted.values)
deviance_res_apriori <- residuals(mod_final_behav, type = "deviance")
fit_dat_fin_apriori <- cbind(fit_dat_fin_apriori, deviance_res_apriori)
fit_dat_fin_apriori %>%
ggplot(aes(sample = deviance_res_apriori)) +
geom_qq() +
geom_qq_line() +
labs(title = "Q-Q plot of deviance residuals")
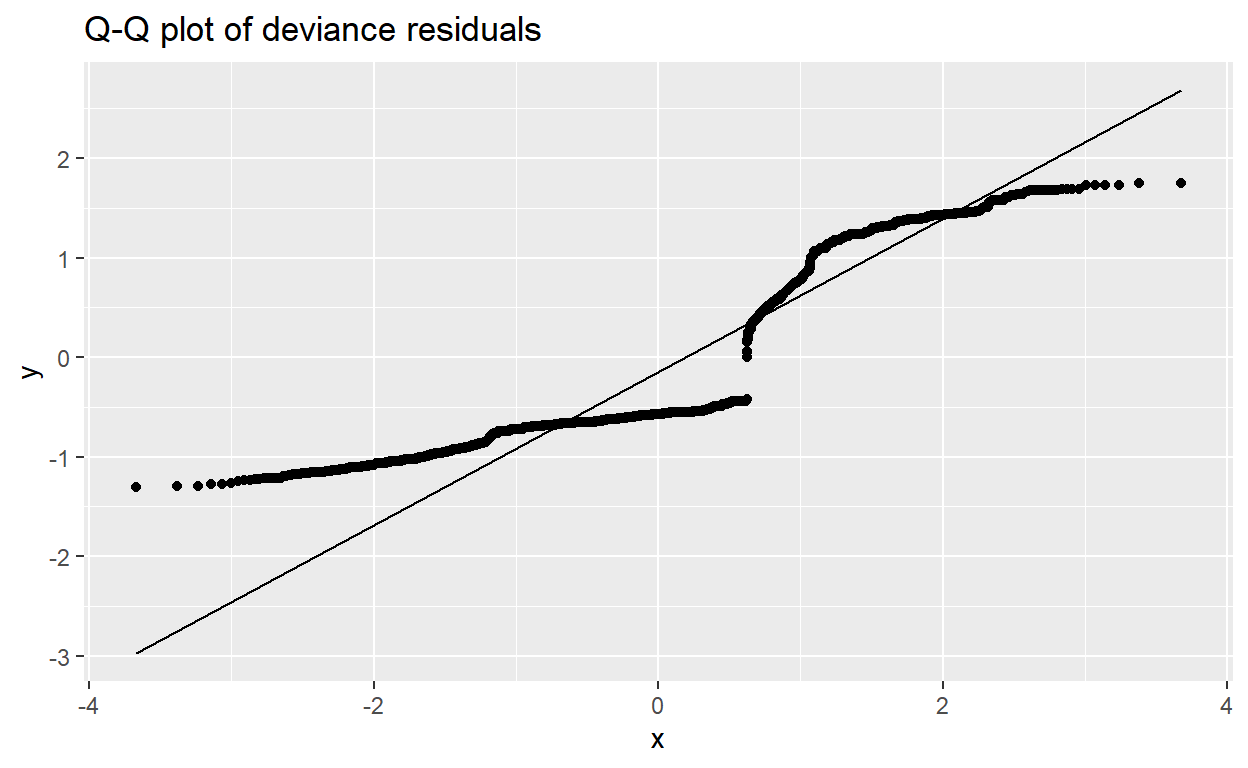
ggsave("Q-Q_final_behav_mod.png", width = 6, height = 4, units = "in")
fit_dat_fin_all <- as.data.frame(MLR_3$fitted.values)
deviance_res_fin <- residuals(MLR_3, type = "deviance")
fit_dat_fin_all <- cbind(fit_dat_fin_all, deviance_res_fin)
fit_dat_fin_all %>%
ggplot(aes(sample = deviance_res_fin)) +
geom_qq() +
geom_qq_line() +
labs(title = "Q-Q plot of deviance residuals")
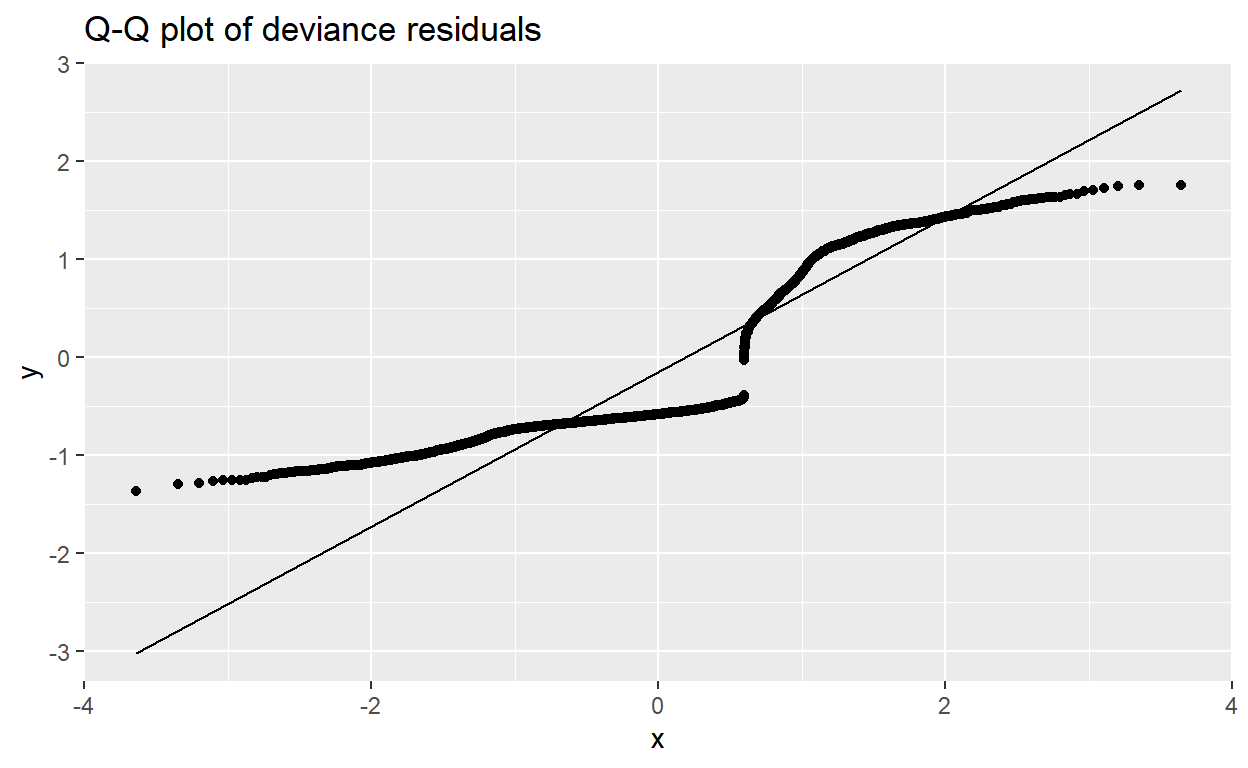
ggsave("Q-Q_all_variables.png", width = 6, height = 4, units = "in")
Under the correct distribution of the response, we expect the points to align with the diagonal line. However, it is usual to have departures from the diagonal in the extremes other than in the center, even under normality. The graph is a little bit strange because we ran Poisson models, but the assumption is met.
Part f-2 : check outliers
Identify the outliers in the final a-priori models:
fit_dat_fin_apriori %>%
ggplot() +
geom_boxplot(aes(y = pearson_res_fin)) +
labs(y="Pearson residuals", title="Boxplot of pearson residuals")
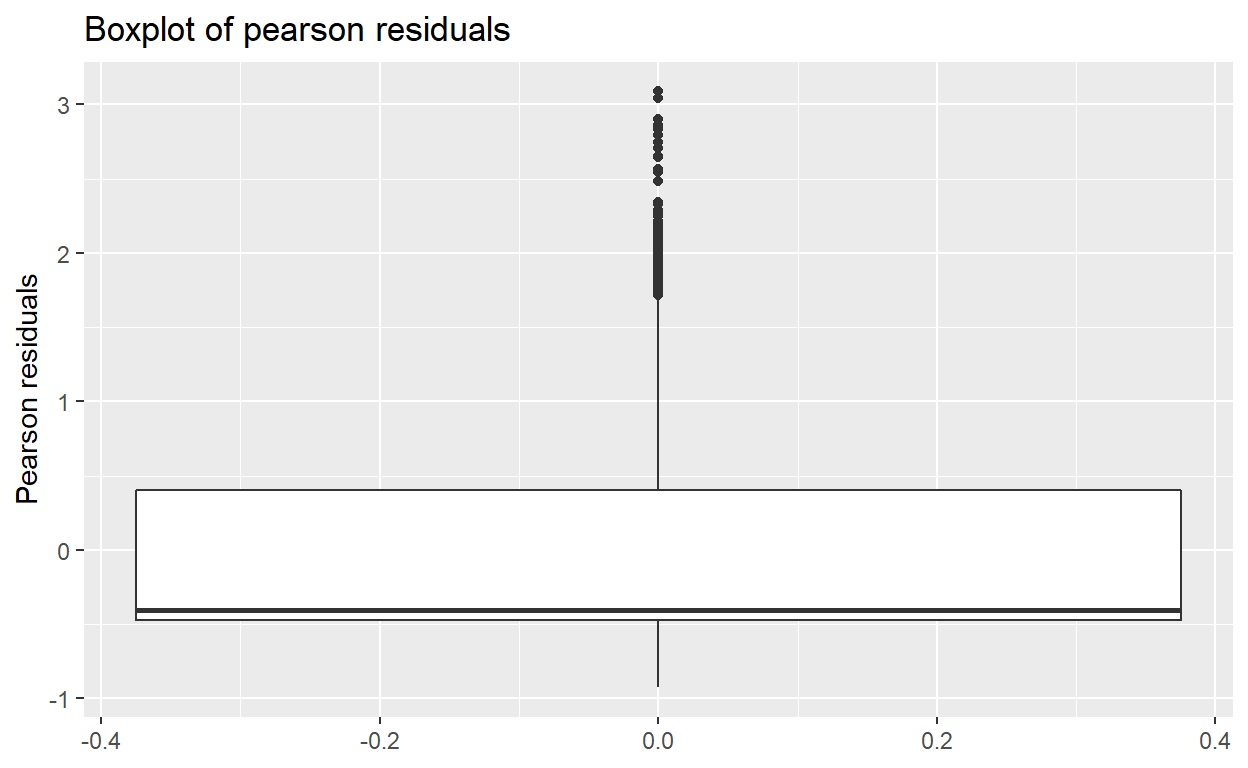
# Looking at the plot we can filter to see which observation is the outlier
outlier_list <- fit_dat_fin_apriori %>%
filter(pearson_res_fin > 2.5)
glimpse(outlier_list)
Rows: 40
Columns: 2
$ `mod_final_behav$fitted.values` <dbl> 0.09910205, 0.09679036, 0.08~
$ deviance_res_apriori <dbl> 1.679707, 1.692335, 1.733906~nrow(outlier_list)
[1] 40#ggsave("outlier_residuals_apriori.png", width = 6, height = 4, units = "in")
Part g : check leverage
fit_dat_fin_apriori <- fit_dat_fin_apriori %>%
mutate(lev = hatvalues(mod_final_behav))
# Boxplot of leverage values
fit_dat_fin_apriori %>%
ggplot() +
geom_boxplot(aes(y = lev)) +
labs(y="Leverage values", title="Boxplot of leverages")
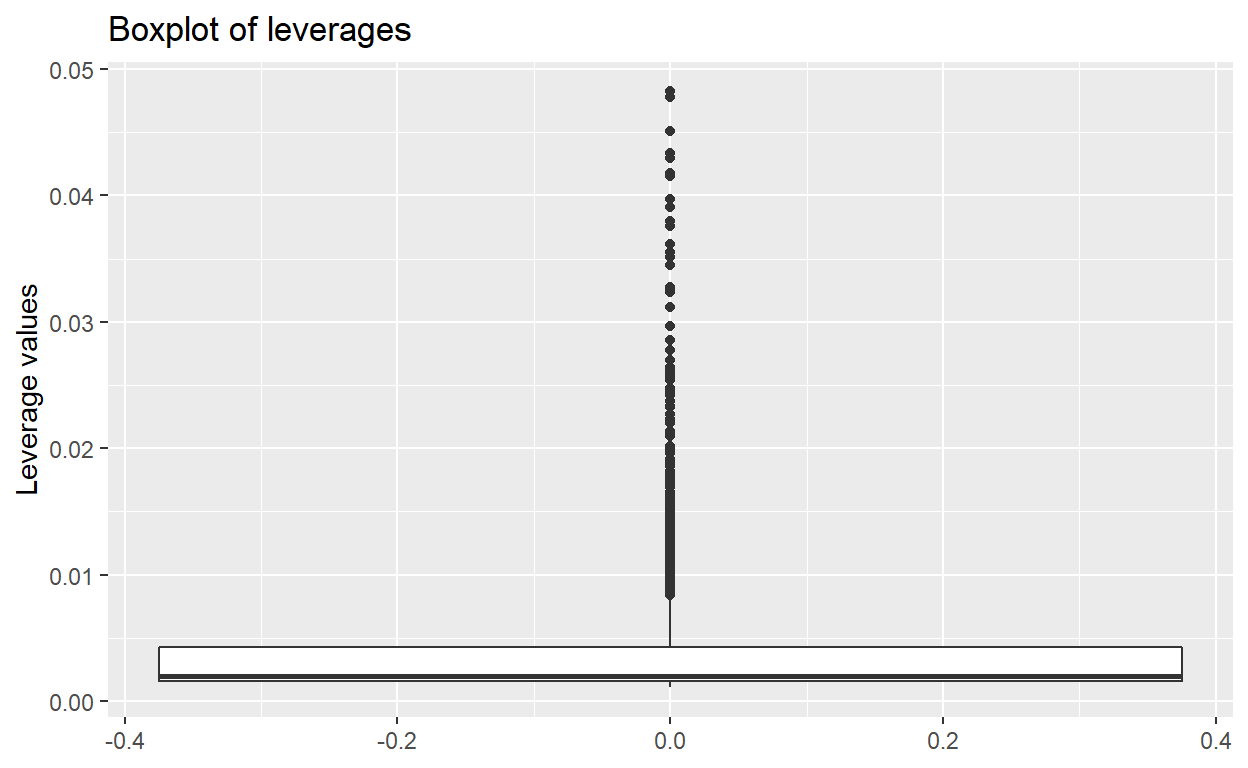
summary(fit_dat_fin_apriori$lev)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.001112 0.001548 0.001979 0.003601 0.004278 0.048211 lev_outliers <- 0.004278 + 1.5*(IQR(fit_dat_fin_apriori$lev))
list_lev_outliers <- fit_dat_fin_apriori %>%
filter(lev > lev_outliers)
glimpse(list_lev_outliers)
Rows: 336
Columns: 3
$ `mod_final_behav$fitted.values` <dbl> 0.5299878, 0.5505493, 0.6055~
$ deviance_res_apriori <dbl> 0.5742631, 0.5429329, 0.4629~
$ lev <dbl> 0.010388046, 0.011440973, 0.~nrow(list_lev_outliers)
[1] 336#ggsave("Leverages_apriori.png", width = 6, height = 4, units = "in")
There are 336 leverage outliers!
Part h: Check model: influence
Part h-1: Make boxplot and list outliers for influence
# Calculate DFITS influence measure -- effect ith obs on overall fit
# Add them to data set
fit_dat_fin_apriori <- fit_dat_fin_apriori %>%
mutate(dfits = dffits(mod_final_behav))
# Boxplot of dfits values
fit_dat_fin_apriori %>%
ggplot() +
geom_boxplot(aes(y = dfits)) +
labs(y="DFITS values", title="Boxplot of DFIT values")
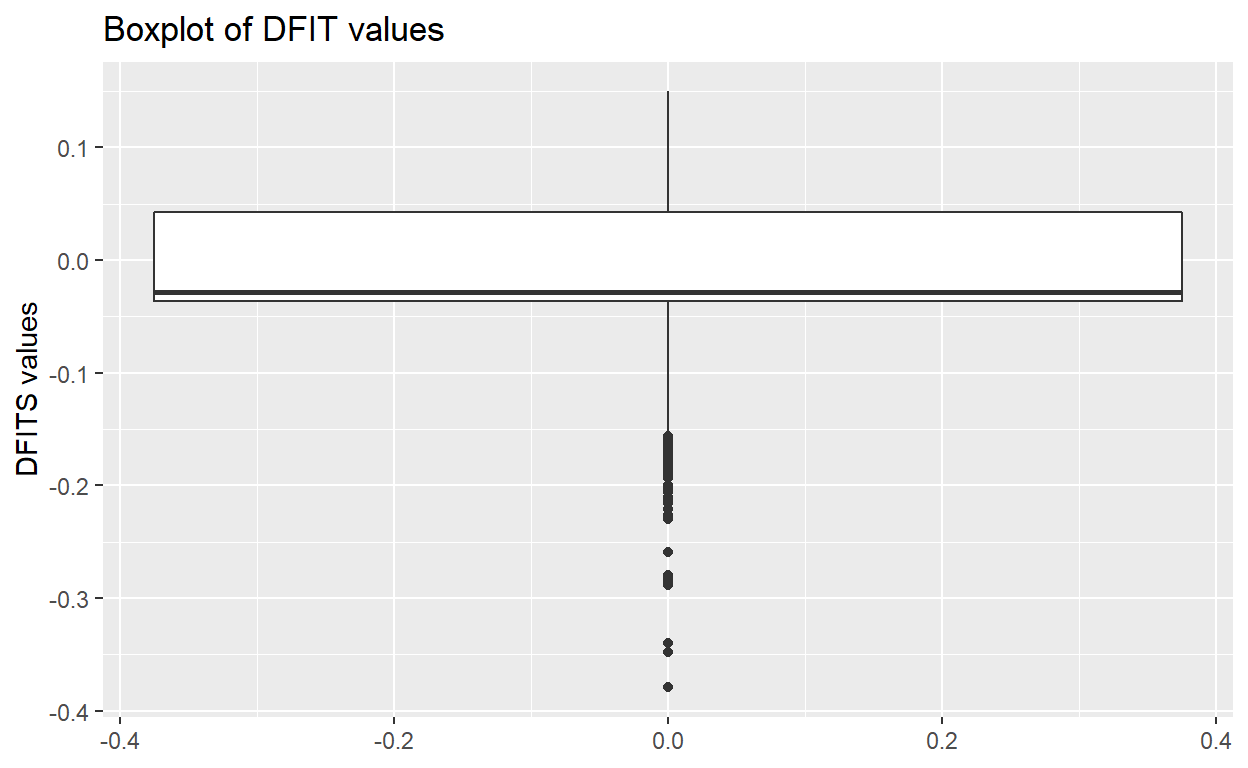
ggsave("dfits_apriori.png", width = 6, height = 4, units = "in")
# Look at outliers
influential_points <- fit_dat_fin_apriori %>%
dplyr::select(dfits) %>%
filter(dfits <= quantile(dfits, .25) - 1.5*IQR(dfits) |
dfits >= quantile(dfits, .75) + 1.5*IQR(dfits)) %>%
arrange(dfits)
glimpse(influential_points)
Rows: 56
Columns: 1
$ dfits <dbl> -0.3788205, -0.3478482, -0.3398676, -0.2887166, -0.285~nrow(influential_points)
[1] 56Part h-2: Leverage -vs- residual squared (L-R) plot
fit_dat_fin_apriori %>%
ggplot(aes(x = pearson_res_fin^2, y = lev)) +
geom_point() +
geom_hline(yintercept = mean(fit_dat_fin_apriori$lev), col="red") +
geom_vline(xintercept = mean(fit_dat_fin_apriori$pearson_res_fin^2), col="red") +
labs(title="Leverage-Residual Plot")
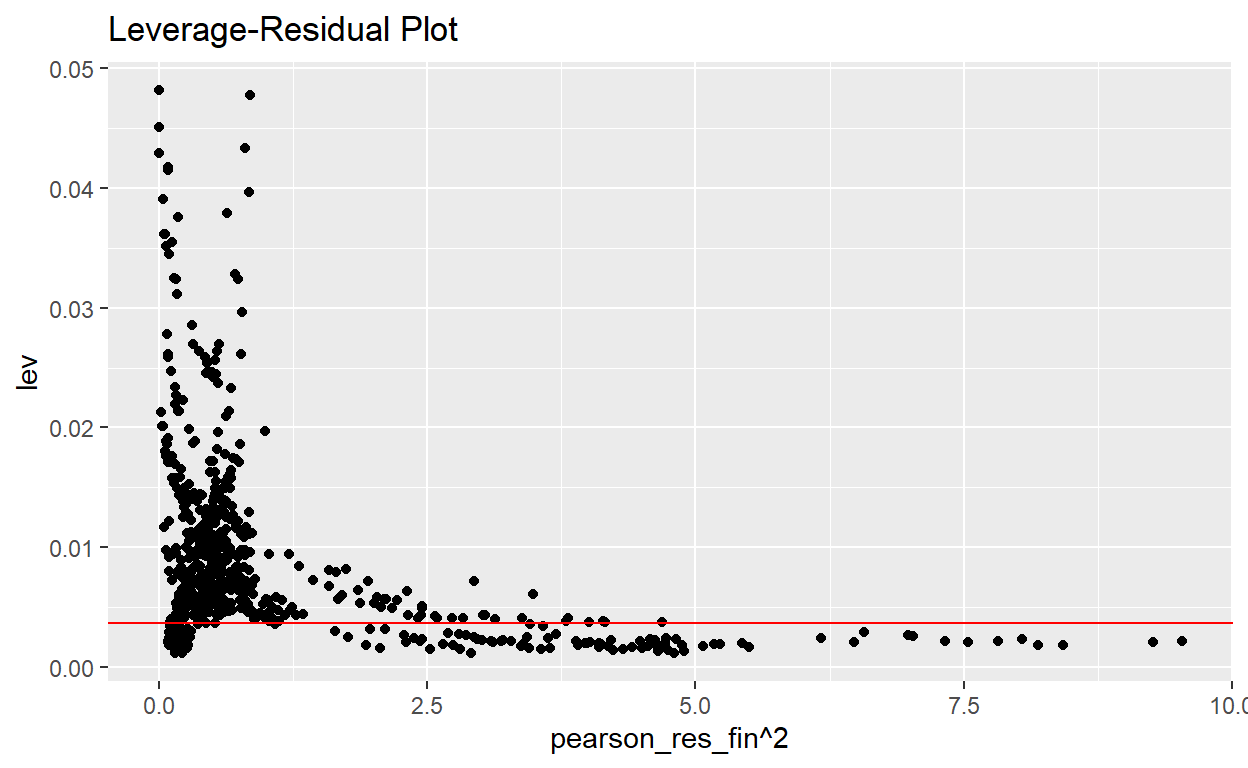
ggsave("L-R plot apriori.png", width = 6, height = 4, units = "in")
Part i: Sensitivity analysis: Re-fit without influential points
Sensitivity analysis conducted on the 8 most influential points:
Create new data set without influential points:
Fit the model without the influential points:
model_final_b_no_outliers <- glm(day_sleep~depress_cat + ageCat_18 + SMQ681 + activity +
raceEthCat + hi_caffeine + heavy_drink2, family=poisson(link="log"), data = unweighted_data)
summary(model_final_b_no_outliers)
Call:
glm(formula = day_sleep ~ depress_cat + ageCat_18 + SMQ681 +
activity + raceEthCat + hi_caffeine + heavy_drink2, family = poisson(link = "log"),
data = unweighted_data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3059 -0.6649 -0.5739 0.3749 1.7463
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.60500 0.15997 -3.782 0.000156 ***
depress_cat.L 0.83543 0.13796 6.056 1.40e-09 ***
depress_cat.Q -0.40609 0.12492 -3.251 0.001151 **
depress_cat.C 0.29800 0.11183 2.665 0.007706 **
depress_cat^4 -0.03835 0.09589 -0.400 0.689213
ageCat_1840-59 -0.18828 0.07594 -2.479 0.013167 *
ageCat_1860+ -0.21188 0.07645 -2.772 0.005579 **
SMQ681 0.10213 0.07482 1.365 0.172250
activity -0.09067 0.06641 -1.365 0.172142
raceEthCatNH Black -0.34672 0.08010 -4.328 1.50e-05 ***
raceEthCatNH Asian -0.78766 0.13358 -5.897 3.71e-09 ***
raceEthCatHispanic -0.36168 0.08289 -4.363 1.28e-05 ***
raceEthCatNH Other/Multiple -0.13766 0.12599 -1.093 0.274537
hi_caffeine 0.11937 0.12200 0.978 0.327873
heavy_drink2 0.03806 0.06676 0.570 0.568567
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2935.0 on 4164 degrees of freedom
Residual deviance: 2599.7 on 4150 degrees of freedom
(1691 observations deleted due to missingness)
AIC: 4847.7
Number of Fisher Scoring iterations: 6coeftest(mod_final_behav, vcov = sandwich)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.604997 0.121445 -4.9817 6.304e-07
depress_cat.L 0.835431 0.081969 10.1920 < 2.2e-16
depress_cat.Q -0.406091 0.075380 -5.3872 7.156e-08
depress_cat.C 0.297997 0.071108 4.1908 2.780e-05
depress_cat^4 -0.038350 0.063182 -0.6070 0.5438610
ageCat_1840-59 -0.188282 0.060499 -3.1122 0.0018573
ageCat_1860+ -0.211885 0.061448 -3.4482 0.0005643
SMQ681 0.102129 0.059907 1.7048 0.0882301
activity -0.090669 0.052991 -1.7110 0.0870746
raceEthCatNH Black -0.346716 0.065189 -5.3187 1.045e-07
raceEthCatNH Asian -0.787660 0.119233 -6.6061 3.946e-11
raceEthCatHispanic -0.361676 0.067043 -5.3947 6.863e-08
raceEthCatNH Other/Multiple -0.137664 0.096014 -1.4338 0.1516323
hi_caffeine 0.119369 0.092434 1.2914 0.1965662
heavy_drink2 0.038062 0.053537 0.7110 0.4771127
(Intercept) ***
depress_cat.L ***
depress_cat.Q ***
depress_cat.C ***
depress_cat^4
ageCat_1840-59 **
ageCat_1860+ ***
SMQ681 .
activity .
raceEthCatNH Black ***
raceEthCatNH Asian ***
raceEthCatHispanic ***
raceEthCatNH Other/Multiple
hi_caffeine
heavy_drink2
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1exp(model_final_b_no_outliers$coefficients)
(Intercept) depress_cat.L
0.5460763 2.3058075
depress_cat.Q depress_cat.C
0.6662495 1.3471573
depress_cat^4 ageCat_1840-59
0.9623758 0.8283812
ageCat_1860+ SMQ681
0.8090580 1.1075267
activity raceEthCatNH Black
0.9133201 0.7070058
raceEthCatNH Asian raceEthCatHispanic
0.4549079 0.6965079
raceEthCatNH Other/Multiple hi_caffeine
0.8713918 1.1267856
heavy_drink2
1.0387961 exp(mod_final_behav$coefficients)
(Intercept) depress_cat.L
0.5460763 2.3058075
depress_cat.Q depress_cat.C
0.6662495 1.3471573
depress_cat^4 ageCat_1840-59
0.9623758 0.8283812
ageCat_1860+ SMQ681
0.8090580 1.1075267
activity raceEthCatNH Black
0.9133201 0.7070058
raceEthCatNH Asian raceEthCatHispanic
0.4549079 0.6965079
raceEthCatNH Other/Multiple hi_caffeine
0.8713918 1.1267856
heavy_drink2
1.0387961 Part j: Check variance inflation
vif(MLR_3) #check VIF of unweighted model with all risk factors
GVIF Df GVIF^(1/(2*Df))
RIAGENDR 1.059197 1 1.029173
ageCat_18 1.223982 2 1.051826
INDFMPIR 1.149586 1 1.072187
SMQ681 1.208305 1 1.099229
raceEthCat 1.225887 4 1.025785
activity 1.086719 1 1.042458
hi_caffeine 1.099705 1 1.048668
BMI_cat 1.114698 3 1.018262
heavy_drink2 1.160023 1 1.077044
depress_cat 1.126430 4 1.014993vif(mod_final) # check VIF of best subset model
GVIF Df GVIF^(1/(2*Df))
depress_cat 1.021293 4 1.002637
raceEthCat 1.044998 4 1.005517
ageCat_18 1.042034 2 1.010347vif(mod_final_behav) # check VIF of a priori model
GVIF Df GVIF^(1/(2*Df))
depress_cat 1.060084 4 1.007320
ageCat_18 1.170830 2 1.040216
SMQ681 1.134808 1 1.065274
activity 1.056344 1 1.027786
raceEthCat 1.134959 4 1.015950
hi_caffeine 1.092136 1 1.045053
heavy_drink2 1.145752 1 1.070398Results
unweighted_data %>%
select(day_sleep, RIAGENDR, ageCat_18, INDFMPIR, SMQ681, raceEthCat, activity, hi_caffeine, BMI_cat, heavy_drink2, depress_cat) %>%
tbl_uvregression(
method = glm,
y = day_sleep,
method.args = list(family = binomial(link="log")),
exponentiate = TRUE,
pvalue_fun = ~style_pvalue(.x, digits = 2)
) %>%
add_global_p() %>% # add global p-value
add_q() %>% # adjusts global p-values for multiple testing
bold_p() %>% # bold p-values under a given threshold (default 0.05)
bold_p(t = 0.10, q = TRUE) %>% # now bold q-values under the threshold of 0.10
modify_caption("Crude Table") %>%
bold_labels()
| Characteristic | N | RR1 | 95% CI1 | p-value | q-value2 |
|---|---|---|---|---|---|
| RIAGENDR | 5856 | 1.20 | 1.10, 1.31 | <0.001 | <0.001 |
| ageCat_18 | 5856 | <0.001 | 0.001 | ||
| 18-39 | — | — | |||
| 40-59 | 0.82 | 0.74, 0.92 | |||
| 60+ | 0.87 | 0.78, 0.96 | |||
| INDFMPIR | 5021 | 0.92 | 0.89, 0.95 | <0.001 | <0.001 |
| SMQ681 | 5132 | 0.85 | 0.76, 0.94 | 0.002 | 0.003 |
| raceEthCat | 5856 | <0.001 | <0.001 | ||
| NH White | — | — | |||
| NH Black | 0.68 | 0.61, 0.76 | |||
| NH Asian | 0.42 | 0.35, 0.49 | |||
| Hispanic | 0.67 | 0.60, 0.75 | |||
| NH Other/Multiple | 0.92 | 0.76, 1.09 | |||
| activity | 5849 | 0.95 | 0.87, 1.05 | 0.31 | 0.31 |
| hi_caffeine | 4339 | 1.41 | 1.16, 1.67 | <0.001 | 0.001 |
| BMI_cat | 5434 | <0.001 | <0.001 | ||
| normal | — | — | |||
| underweight | 1.07 | 0.71, 1.51 | |||
| overweight | 1.05 | 0.92, 1.20 | |||
| obese | 1.44 | 1.28, 1.62 | |||
| heavy_drink2 | 5120 | 1.23 | 1.12, 1.35 | <0.001 | <0.001 |
| depress_cat | 5068 | <0.001 | <0.001 | ||
| depress_cat.L | 2.42 | 2.02, 2.79 | |||
| depress_cat.Q | 0.61 | 0.52, 0.70 | |||
| depress_cat.C | 1.23 | 1.08, 1.40 | |||
| depress_cat^4 | 0.91 | 0.82, 1.02 | |||
|
1
RR = Relative Risk, CI = Confidence Interval
2
False discovery rate correction for multiple testing
|
|||||
Best subset model included race categories, age categories, and depression score categories as predictors. The final model was the model including behavioral variables selected a-priori, along with age and depression score which were identified through the AI model. This final model best suits the epidemiological question at hand: which risk factors are most important in the relationship with excessive daytime sleepiness, with a special emphasis on modifiable lifestyle factors?
- The predictors in the final model: age categories, race categories, depression score categories, current smoking, weekly moderate to vigorous activity, high caffeine intake, and heavy alcohol use
The dataset was large, so the model is still parsimonious with many predictors. All candidate models had Pearson’s Goodness of Fit p-values equal to 1, so all fit the data very well. None of the variables showed signs of collinearity for any of the candidate models.
Results from the final model:
mod_final_behav %>%
tbl_regression(exponentiate = TRUE) %>%
add_global_p() %>% # add global p-value
add_q() %>% # adjusts global p-values for multiple testing
bold_p() %>% # bold p-values under a given threshold (default 0.05)
bold_p(t = 0.10, q = TRUE) %>% # now bold q-values under the threshold of 0.10
modify_caption("Final model") %>%
bold_labels()
| Characteristic | IRR1 | 95% CI1 | p-value | q-value2 |
|---|---|---|---|---|
| depress_cat | <0.001 | <0.001 | ||
| depress_cat.L | 2.31 | 1.73, 2.98 | ||
| depress_cat.Q | 0.67 | 0.52, 0.84 | ||
| depress_cat.C | 1.35 | 1.08, 1.68 | ||
| depress_cat^4 | 0.96 | 0.80, 1.16 | ||
| ageCat_18 | 0.010 | 0.023 | ||
| 18-39 | — | — | ||
| 40-59 | 0.83 | 0.71, 0.96 | ||
| 60+ | 0.81 | 0.70, 0.94 | ||
| SMQ681 | 1.11 | 0.96, 1.28 | 0.2 | 0.2 |
| activity | 0.91 | 0.80, 1.04 | 0.2 | 0.2 |
| raceEthCat | <0.001 | <0.001 | ||
| NH White | — | — | ||
| NH Black | 0.71 | 0.60, 0.83 | ||
| NH Asian | 0.45 | 0.35, 0.59 | ||
| Hispanic | 0.70 | 0.59, 0.82 | ||
| NH Other/Multiple | 0.87 | 0.68, 1.11 | ||
| hi_caffeine | 1.13 | 0.88, 1.42 | 0.3 | 0.4 |
| heavy_drink2 | 1.04 | 0.91, 1.18 | 0.6 | 0.6 |
|
1
IRR = Incidence Rate Ratio, CI = Confidence Interval
2
False discovery rate correction for multiple testing
|
||||
- Belonging to older age groups (40-59 years & 60+ years) conferred a decreased risk of excessive daytime sleepiness when compared to a referent group of 18-39 years, contrary to what is expected based on the literature
- This may indicate that age-differential lifestyle factors confound the relationship between age and sleep quality.
- There was also an association in the opposite direction of to what is expected for race categories.
- When compared to white individuals, Hispanic, Asian, and Black individuals have a decreased risk of excessive daytime sleepiness
- Perhaps the relationship is confounded by social factors not accounted for in the study
- When compared to white individuals, Hispanic, Asian, and Black individuals have a decreased risk of excessive daytime sleepiness
- Associations with the most potential for intervention were mild and moderate to severe depression, caffeine intake, and obesity
- The direction of the association of depression score with excessive daytime sleepiness varied by severity, which may be due to low sample sizes in severity categories
- Some covariates previously presented as risk factors for poor sleep quality in the literature that were not replicated in this study were heavy alcohol use, current tobacco smoking, and participation in weekly moderate to vigorous physical activity
Conclusions and future directions
Conflicting results emphasize the need for more research is needed to uncover the links between age, race, alcohol use, tobacco smoking and exercise on sleep quality
High daily caffeine consumption is a modifiable risk factor that could play a role in causing excessive sleepiness during the day.
Based on these results and the results of previous research, it may be clinically advisable to address sleep hygiene in people with depression and obesity to prevent future morbidity and mortality.